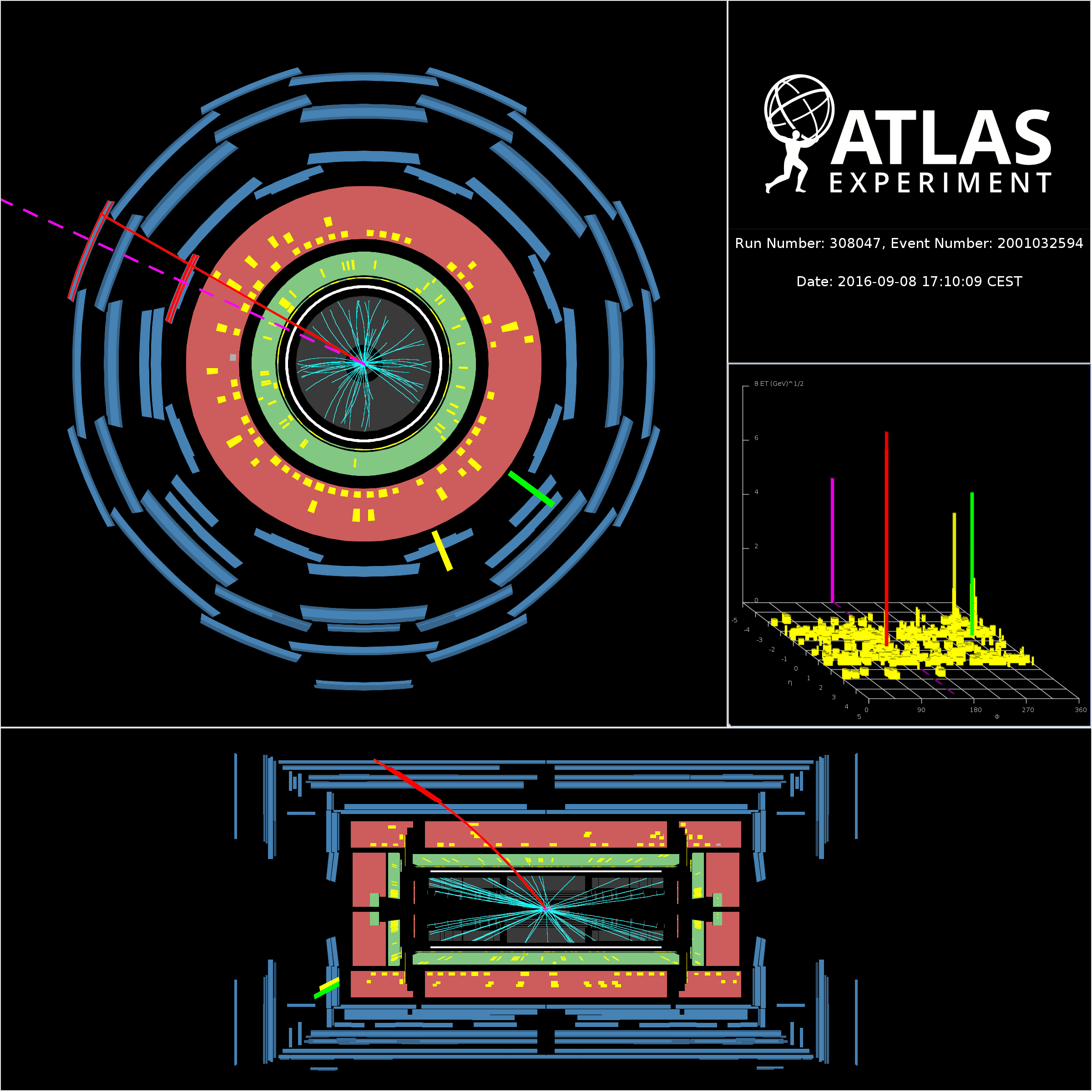
In 2017, the ATLAS and CMS Collaborations announced the detection of a process in high-energy proton–proton collisions that had not been observed before: the vector boson scattering. It results in the production of two W particles with the same electric charge as well as two collimated sprays of particles called “jets" (see Figure 2). The observation of vector boson scattering didn't receive as much attention from the media as the Higgs discovery in 2012, even though it was an important event for the particle physics community. Another missing piece of the big puzzle had been found – the puzzle that is the mathematical description of the microscopic world (see Figure 1).

The W⁺ and W^– bosons are unstable particles, which decay (transform) into a lepton and an antilepton or a quark and an antiquark with a mean lifetime of only a few 10^-25 seconds. They have integer spin (characteristic of bosons) and are carriers of the weak force. Though the weak force is not directly experienced in everyday life, it is nevertheless important as it is responsible for radioactive β decay, which plays a role in the fusion of hydrogen into helium that powers the Sun's thermonuclear process.

To appreciate the importance of this discovery, it is instructive to follow the history of how and why the W⁺ and W^– bosons were introduced; it illustrates nicely how the interplay between experimental information, theoretical models and mathematical principles drives progress in physics.

Enrico Fermi originally formulated a mathematical description of the weak force in 1933 as a “contact interaction” between particles, occurring at a single point without a carrier particle propagating the force. This formulation successfully described the known experimental observations, including the radioactive β decay for which it was developed. However it was soon realised that its predictions at high energy, a regime not yet experimentally accessible at that time, were bound to fail.

Indeed, Fermi's theory predicts that the production rate of some processes caused by the weak force – such as the elastic scattering of neutrinos on electrons – increases linearly with the neutrino energy. This continuous growth, however, leads to the violation of a limit derived from the conservation of probability in a scattering process. In other words, predictions become unphysical at a high enough energy. To overcome this problem, physicists modified Fermi's theory by introducing “by hand" two massive spin-one (“vector”) charged particles propagating the interaction between neutrinos and electrons, dubbed “intermediate vector bosons". This development came well before the discovery of the W bosons decades later.

So even if the discovery of the long-awaited W^± bosons in 1983 – and, five months later, of a neutral companion, the Z boson – didn't come as a real surprise to physicists, it was certainly an epochal experimental achievement. Fermi’s theory remains an example of an effective theory valid only at low energy (well below the mass of the force carrier boson) – an approximation of a more general, universally valid theory.

Along this line, the search for a consistent description of the fundamental forces between the ultimate constituents of matter has led to the Standard Model of particle physics: a mathematical construction based on fundamental principles and experimental observations. The Standard Model provides a coherent, unified picture of three of the four fundamental interactions, namely the electromagnetic, weak and strong force. The fourth force, not included in the Standard Model, is gravity. So far, the Standard Model has been successful at describing a myriad of experimental measurements in the microscopic world. Its success is, by all means, mind blowing.

We do not know why natural phenomena are so well described by mathematical entities and relations but, experimentally, we know that it works. Just as Galileo said four hundred years ago, the big book of Nature is written in a mathematical language^[1] – the Standard Model and Einstein’s theory of gravity, for example, are additional chapters of this book.

Particle physics makes use of a theoretical tool in which all particles are represented mathematically by quantum fields. These entities encode properties like spin and mass of a particle. In the Standard Model, the existence of the electromagnetic, weak and strong force carriers follows from the invariance of the behaviour of quantum fields under a “local gauge transformation". This is a transformation from one field configuration to another, which can be imagined as a rotation in an abstract mathematical space. The parameters of the transformation may vary from point to point in space-time, and thus the transformation is defined as “local”. Gauge invariance or gauge symmetry is the lack of changes in measurable quantities under gauge transformations, despite the quantum fields (which represent particles) being transformed.

Gauge invariance holds if spin-one particles are introduced, which interact in a well-defined manner with the elementary constituents of matter such as electrons and quarks (constituents of the proton and neutron, or, more generally, of hadrons). These spin-one particles are interpreted as “the carriers of the interaction” between the matter particles, with the photon the carrier for the electromagnetic force, the W^–, W⁺ and Z bosons for the weak force, and eight gluons for the strong force. These are the (intermediate) vector bosons introduced above.

In this way, the Standard Model forces (or interactions) emerge in a very elegant manner from one general principle, namely a fundamental symmetry of Nature. Interestingly enough, in the model, the electromagnetic and weak interactions manifest themselves at high energy as different aspects of a single “electroweak" force, while at low energy the weak interaction remains feebler than the electromagnetic interaction. As a consequence, the photon, Z boson and W^± bosons are collectively named “electroweak gauge bosons".

In the example above, Fermi’s followed a bottom-up approach: going from an observation to a mathematical description (a contact-interaction theory), which was modified “by hand" with few additions to obey the general principle of probability conservation (known as “unitarity” in physics). Starting from this premise, the work of many physicists consequently led to a more general theory. One in which the description of the fundamental forces follows the opposite path: predictions are obtained from fundamental principles (as gauge invariance) in a mathematically and physically coherent framework.^[2] The interplay between these two ways of developing knowledge had been common in physics since before Newton's time, and still valid today.

In both cases, a theory is successful not only when it describes the known experimental facts, but also when it has predictive power. The Standard Model possesses both virtues and examples of its predictive power include the discoveries of the Higgs boson and the neutral kind of weak interaction mediated by the Z boson.

As a matter of fact, the Standard Model tells us (much) more: the quantum fields representing the new spin-one particles will also transform under a local gauge transformation. To ensure that the measurable quantities describing their behaviour do not change (gauge invariance, mentioned above), interactions among the carriers of the weak force must also exist, as well as among the carriers of the strong force. These self-interactions may involve three or four gauge bosons. No self-interaction among photons is possible, except indirectly through virtual processes involving intermediate particles such as electrons, as observed in a dedicated ATLAS measurement.

The process first observed by the ATLAS and CMS Collaborations in 2017, characterised by the presence of two W bosons with the same electric charge and two jets, is a signature of the occurrence of an electroweak interaction. The dominant part of the process is due to the self-interaction among four weak gauge bosons; another central prediction of the Standard Model finally confirmed by the LHC experiments. This self-interaction manifests as a “vector boson scattering", where two incoming gauge bosons interact and produce two, potentially different, gauge bosons as final state particles. The production rate of this electroweak process is very low – lower than that of Higgs boson – which is why it was observed only recently. And just like the Higgs boson discovery, the observation of this process didn't come out of the blue.

At the Large Electron–Positron (LEP) collider, which operated at CERN between 1989 and 2000 in what is today the LHC tunnel, physicists had already observed the self-interaction among three gauge bosons. They measured the production of a pair of gauge bosons of opposite charge, a W⁺ and a W^– boson, in the collisions of beams of electrons and positrons, the antiparticle of the electron. According to the Standard Model, three main processes contribute to this production. They proceed via the exchange of either a photon, neutrino or Z boson between the electron and positron of the initial state and the W pair of the final state (Figure 3).

The exchange of a photon or a Z boson occurs via the self-interaction of three weak gauge bosons: WWγ and WWZ, respectively. The main point here is that without considering all three processes, the calculated production rate would grow continuously with energy, leading to the already encountered unphysical behaviour. The observation of this process at LEP, with a production rate consistent with the Standard Model prediction, therefore confirmed the existence of a self-interaction among three bosons.

It is striking that the theory predicts the structure of each underlying process such that, even though each of them gives to the calculated production rate a contribution which at high energy becomes unphysical, violating unitarity, the unphysical behaviour cancels out when all of the processes are considered together.

So far, so good – but there’s a catch. The W^± and Z bosons observed and identified by experiments as the carriers of the weak interaction are massive, yet gauge invariance is only preserved if the carriers are massless. Should physicists give up the principle of gauge invariance to reconcile the theory with experimental facts?

A solution to this puzzle was proposed in 1964, postulating the existence of a new spin-zero (“scalar”) field with a slightly more complex mathematical structure. While the basic laws of the forces remain exactly gauge symmetric, in the sense explained above, Nature has randomly chosen (among many possibilities) a particular lowest-energy state of this field, breaking with this choice the gauge symmetry in a limited way, called “spontaneous”.

The consequences are dramatic. Out of this new field, a new particle emerges – the scalar Higgs boson – and the W^± and Z bosons become massive. Physicists now believe that gauge symmetry was not always spontaneously broken. The universe transitioned from an “unbroken phase” with massless gauge bosons to our current “broken phase” during expansion and cool-down, a fraction of a second after the Big Bang.

The discovery of the Higgs boson in 2012 by the ATLAS and CMS Collaborations is a great success of the Standard Model theory, especially when considering that it was found to have the mass that indirect clues were pointing to. While the Higgs boson mass is not predicted by theory, the existence of the Higgs boson with a given mass leaves a delicate footprint in natural phenomena such that, if measured very precisely (as was done at LEP and at Tevatron, the smaller predecessor of the LHC at Fermilab, nearby Chicago, USA), physicists could derive constraints on its mass. The Higgs boson’s discovery was thus an experimental prowess as well as a consecration of the Standard Model. It emphasized the remarkable role of the precision measurements at LEP, even though the energy of that accelerator was not high enough to directly produce the Higgs boson.

Obviously, the story doesn't end here. Solid indications exist that the Standard Model is not complete and that it must be encompassed in a more general theory. This possibility is not surprising. As Fermi’s weak interaction theory exemplifies, history has shown that a theory’s validity is related to the energy range (or, equivalently, size of space) accessible by experiments.

More generally, classical mechanics is appropriate and predictive for the macroscopic world, when the speed of the objects is small with respect to the speed of light. To describe the microscopic world, however, quantum mechanics must be invoked, and the special theory of relativity must be applied to appropriately describe the behaviour of objects moving close to light speed.

How can physicists find experimental signs that may help to formulate a more general theory than the Standard Model?

A valuable approach is to directly search collision events for particles not included in the Standard Model. However this is inherently limited: only particles with a mass at or below the collision energy can be directly produced, due to the fundamental principle of energy conservation and following the equivalence between mass and energy. Alternative avenues, which suffer less from this limitation but are indirect, include performing very precise measurements of fundamental parameters of the Standard Model or measuring rare processes to look for deviations with respect to theoretical predictions. Such measurements are able to explore a higher energy domain, as the LEP Higgs-boson example showed.

Vector boson scattering is one of these rare processes. It is special because closely related to the Higgs mechanism, and able to shed light on unexplored corners of Nature at the highest energy available in a laboratory. Similar to the LEP vector-boson study described above, vector boson scattering is expected to proceed via several processes, this time including the self-interaction of four gauge bosons as well as the exchange of a Higgs boson (see Figure 4). Without accounting for all of the processes, the calculated scattering rate grows indefinitely with energy, leading to the above-mentioned unphysical behaviour (violation of unitarity).

It could be argued that this question is already settled, since we know that the Higgs boson exists. The key issue is that the way in which the Higgs boson interacts with the gauge bosons in the Standard Model is exactly what is required to moderate the growth of the scattering rate at high energy; a minimal deviation of the Higgs mechanism from the Standard Model prediction could result in an apparent breakdown of unitarity.

Vector boson scattering would then occur at a rate different from what is predicted by the Standard Model, and unitarity would have to be recovered by a yet-unknown mechanism. The study of vector boson scattering thus allows physicists to investigate the Higgs mechanism in the highest energy domain accessible, where there may be signs of new physics.

The LHC is the perfect place to look for rare processes like vector boson scattering, as it collides protons with the highest energy and rate ever reached. Furthermore, the ATLAS and CMS experiments are designed to select and record these rare events.

As weak gauge bosons are extremely short-lived particles, experiments search for the scattering of vector bosons by looking for the production of two jets and two lepton–antilepton pairs in proton-proton collisions. Imagine this as two gauge bosons being emitted by the quarks from each of the incoming LHC proton beams. These gauge bosons subsequently scatter off each other and the bosons emerging from this interaction promptly decay (see Figure 2). The quarks are subsequently deflected and appear in the detector as jets of particles, typically emitted at a relatively small angle with respect to the beam direction. This is called an “electroweak” process as it is mediated by electroweak gauge bosons.

The experimental signature of vector boson scattering is therefore characterised by the presence of the decay particles of the two bosons, accompanied by two jets with large angular separation. The W and Z bosons predominantly decay into a quark and antiquark pair. Nevertheless, the search of these rare events preferentially exploits the decays into a lepton and an anti-lepton because a concurrent process, the multi-jet production, being mediated by the strong interaction has an overwhelming rate and obscures processes with a much smaller rate.

Still, the search for vector boson scattering is very challenging. This is not only because the rate of the process is low – accounting for only one in hundreds of trillions of proton–proton interactions – but also because, even making use of the leptonic decays, several “background” processes produce the same kinds of particles in the detector, mimicking the process’ signal.

Due to its high rate, a particularly challenging background process is one in which the jets accompanying the decay products of the gauge bosons arise as a result of the strong-force interaction. The impact of this background with respect to the signal depends on the kind of gauge bosons which scatter. When they are W bosons with the same electric charge, the production rate of the two processes (signal and background) is comparable.

For this reason, same-charge WW production is considered the golden channel for experimental measurements and was the first target for the ATLAS Collaboration to study vector-boson-scattering processes. ATLAS physicists reported for the first time strong hints of the process in a 2014 paper – a milestone in the LHC physics programme. However, it took three more years to arrive at an unambiguous observation, passing the five-sigma threshold that particle physicists use to define a discovery and corresponding to a probability of less than one in 3.5 million that a signal observation could be due to a mere upward statistical fluctuation of the number of background events. In the years between the first hint and discovery, the LHC was upgraded to increase its proton–proton collision energy – from 8 TeV to 13 TeV – as well as its collision rate – yielding about six times more collected data. These improvements made observation of vector boson scattering possible – the era of its study had at last begun.

However, not all electroweak bosons are equal. While the observation of two same-charge W bosons has allowed physicists to start testing the interaction of four W bosons (WWWW, Figure 2), the quest to test other self-interactions remained. The Standard Model only allows a specific set of combinations of four-gauge-boson self-interactions: WWWW, WWγγ, WWZγ and WWZZ, forbidding interactions among four neutral bosons.

Not all of these electroweak interactions are predicted to have the same strength and, because of this, probing them requires identifying processes that are less and less frequent. Similarly to the case of two same-charge W bosons, electroweak processes involving two jets and a WZ pair, a Zγ pair, or a ZZ pair are increasingly rare or have significantly larger backgrounds. Hunting for such processes among the billions of proton–proton collisions recorded by ATLAS requires physicists to look for subtle differences in order to distinguish a signal from very similar background processes occurring at much higher rates.

While such a task was commonly regarded as requiring a much larger amount of data than collected so far, the LHC experiments used artificial-intelligence algorithms to distinguish between the sought-after signal and the much larger background. Thanks to such innovations, in 2018 and 2019, ATLAS reported the observations of WZ and ZZ electroweak production, and saw a hint of the Zγ process. Suddenly, this brand-new field saw a surge in the number of processes that could be used to probe the self-interaction of gauge bosons.

The most recent addition is ATLAS’ observation of two W bosons produced by the interaction of two photons, each radiated by the LHC protons. This phenomenon occurs when the accelerated protons skim each other, producing extremely high electromagnetic fields, with photons mediating an electromagnetic interaction between them. Such an interaction is only possible when quantum mechanical effects of electromagnetism are taken into account.

This is a direct and clean probe of the γγWW gauge bosons interaction. A peculiarity of this process is that the protons participate as a whole and can remain intact after the interaction; this is very different from inelastic interactions where the quarks, the protons’ constituents, are the main actors (see Figure 2).

Table 1 summarises the processes that are used to study vector boson scattering at the LHC. It also shows the four bosons involved in the self-interaction. The study of each process provides a different test of the Standard Model, as modifications of the theory can differently alter the strength of the self-interactions.

Now, ten years on from the first high-energy collisions took place in the LHC, the study of the vector boson scattering is a very active field – though still in its adolescence, both from the experimental and theoretical point of view. Experimentally, the size of the available signal sample is limited. The upcoming data-taking period (from 2022 to 2024) and the high-luminosity phase of the LHC (starting in 2027) will increase the amount of collected data by more than a factor two and by an additional factor of ten, respectively. An extensive upgrade of the LHC experiments is also ongoing, which will improve further the detection capabilities for the vector-boson-scattering processes.

In parallel, physicists will continue to improve their analysis methods, relying on more and more advanced artificial-intelligence algorithms to disentangle the rare signal processes from the abundant backgrounds. Physicists are also employing advanced calculation techniques to improve the precision of Standard Model predictions to match the increased measurement precision.

Furthermore, a bottom-up approach is being introduced which follows in the footsteps of Enrico Fermi. Physicists have developed a theoretical framework that allows new mathematical terms, respecting basic conservation rules and symmetries, to be added “by hand" to the Standard Model, without relying on a specific new physics model. These terms change the predictions in the high-energy regime where new physics could be expected (Figure 5). The simplest form of this approach is called Standard Model Effective Field Theory.

Even though we know that an effective theory cannot work at an arbitrary high energy scale, history has shown that, supplemented by measurements, it can provide useful guidance at lower energy. Different production-rate measurements – including those of the Higgs boson, boson self-interactions and the top quark – can be, separately or simultaneously, compared to predictions in the same effective theoretical framework.

It would be a sensation if more precise measurements indicated that such new terms are necessary to describe the data. It would be a sign of physics beyond the Standard Model and indication of the direction to take in order to develop a more complete theory, depending on which kinds of terms are needed. The interplay between experimental observations and models in the quest for a complete theory would continue.

Ultimately, all ongoing experimental collider and non-collider studies in particle physics will contribute to building knowledge – be they direct searches for new particles, precision measurements exploiting the power of quantum fluctuations or studies of rare processes. This experimental work is complemented by ever more precise theoretical calculations. In this task, the next generation of powerful particle accelerators now being planned are indispensable tools to find new phenomena that would help us understand the remaining mysteries of the microscopic world.

About the Authors

Lucia Di Ciaccio is a Professor of Physics at the University of Savoie Mont Blanc (France) and member of the ATLAS Collaboration. During her career she has worked on different topics, including lepton and hadron collider physics. Her present research activity deals with the search for signs of new physics phenomena in the multiple gauge boson sector. Simone Pagan Griso is a staff scientist at the Lawrence Berkeley National Laboratory and member of the ATLAS Collaboration. His research topics range from measurements of rare phenomena predicted by the Standard Model to direct searches of new particles that only exist in extension of the Standard Model theory, with emphasis on signatures that require the development of dedicated charged-particle reconstruction algorithms and innovative analysis techniques.

[1] Il Saggiatore (The Assayer) is a book published by Galileo Galilei in October 1623 and is considered to be one of the milestones of the scientific method, propagating the idea that Nature must described and understood using mathematical tools rather than scholastic philosophy, as generally was believed at the time.

[2] In some cases the postulated principles are inspired by experimental facts, like, for example, the measurement of the speed of light for the theory of special relativity.

Further reading

Scientific results

• Observation of electroweak production of a same-sign W boson pair in association with two jets in proton–proton collisions at 13 TeV with the ATLAS detector (Phys.Rev.Lett. 123 (2019) 16, 161801, arXiv: 1906.03203)
• Observation of electroweak W^±Z boson pair production in association with two jets in proton–proton collisions at 13 TeV with the ATLAS detector (Phys. Lett. B 793 (2019) 469, arXiv:1812.09740)
• Observation of electroweak production of two jets and a Z-boson pair with the ATLAS detector at the LHC (Submitted to NPHYS, arXiv: 2004.10612)
• Evidence for electroweak production of two jets in association with a Zγ pair in proton–proton collisions at 13 TeV with the ATLAS detector (Phys. Lett. B 803 (2020) 135341, arXiv:1910.09503)
• CMS Collaboration: Observation of Electroweak Production of Same-Sign W Boson Pairs in the Two Jet and Two Same-Sign Lepton Final State in Proton-Proton Collisions at 13 TeV (Phys. Rev. Lett. 120 (2018) 081801, arXiv: 1709.05822)

News articles

• ATLAS observes W-boson pair production from light colliding with light, Physics Briefing, August 2020
• ATLAS observes light scattering off light, Physics Briefing, March 2019
• The Higgs boson: the hunt, the discovery, the study and some future perspectives, ATLAS Feature, July 2018
• The rise of deep learning, CERN Courier, July 2018
• ATLAS finds evidence for the rare electroweak W±W± production, Physics Briefing, September 2014
• The LEP story, CERN press, October 2000