Exploring the nature of the “ridge” in small systems
28 August 2017 | By
When ultra-relativistic heavy ions collide, a new state of hot and dense matter – the quark–gluon plasma (QGP) – is created. One of the key features for this state is the observation of long-range azimuthal angle correlations between particles emitted over a wide range of pseudorapidity (η). This phenomenon is often referred to as the “ridge”.
The ridge was first discovered in ion–ion collisions, but later was also observed in smaller systems such as proton–proton and proton–ion collisions. The ridge in large systems is commonly interpreted as the result of flow of the QGP medium created in the overlap region of the colliding nuclei.
The origin of the ridge in smaller systems continues to generate considerable debate in the community. An important question about the ridge is whether it is a collective phenomenon involving all of the particles in the event, or if it arises merely from contributions from a handful of particles, such as resonance decays, jets, or multi-jet production (so-called “non-flow”). Results from smaller collision systems have demonstrated that the contributions from these non-collective sources, in particular from jets and dijets, are large and their evaluation poses many challenges and may lead to differences in results among various experiments.
An important question about the ridge is whether it is a collective phenomenon involving all of the particles in the event, or if it arises merely from contributions from a handful of particles.
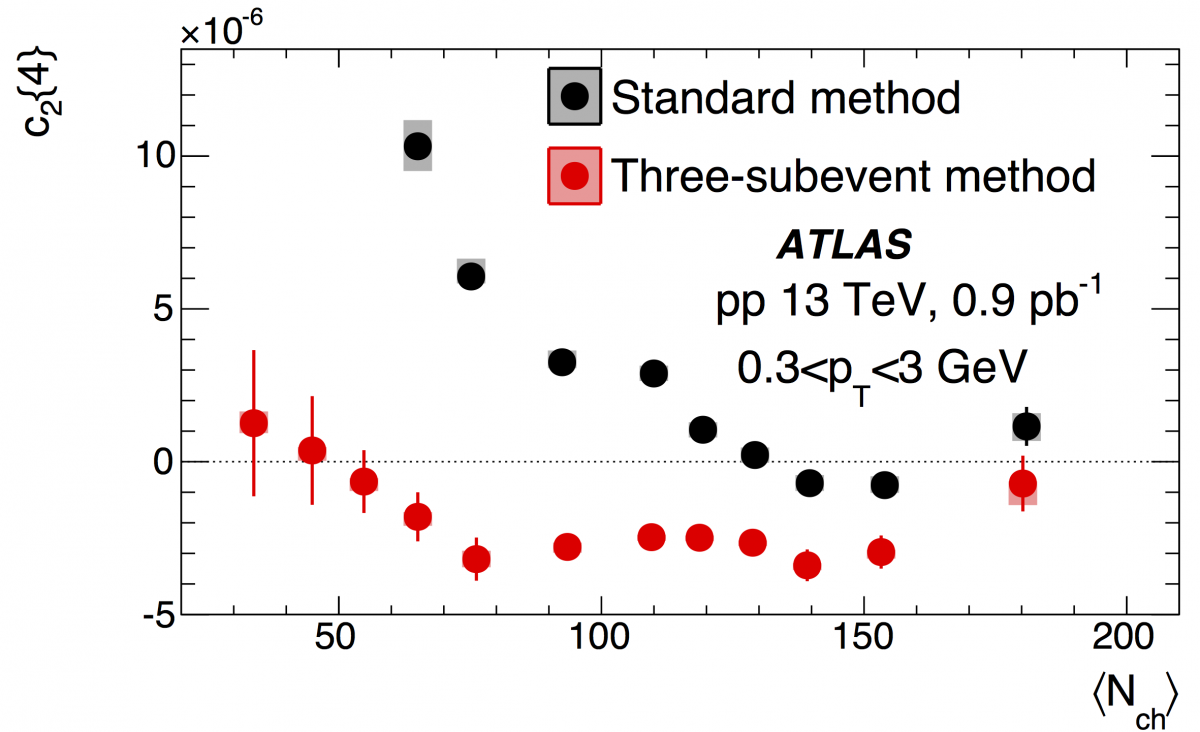
The collective nature of the ridge is often studied using multi-particle correlation techniques, particularly using statistical variables (cumulants) to remove lower-order correlations involving fewer particles. However, previous studies show that non-collective contributions in small systems are large and cannot be suppressed adequately with standard methods.
Recently, an improved cumulant method based on the correlation between particles from different subevents has been proposed to further reduce the non-collective correlations. Using this “subevent cumulant” method, ATLAS has successfully measured the four-particle cumulant and the corresponding elliptic flow coefficient, v2{4}, in proton-proton collisions at 5.02 and 13 TeV, as well as proton-lead collisions at 5.02 TeV (see figures for results from proton-proton collisions at 13 TeV). Previous results for both variables in proton-proton collisions, obtained with the standard cumulant method, are influenced by substantial non-flow correlations, as shown by Figure 1.
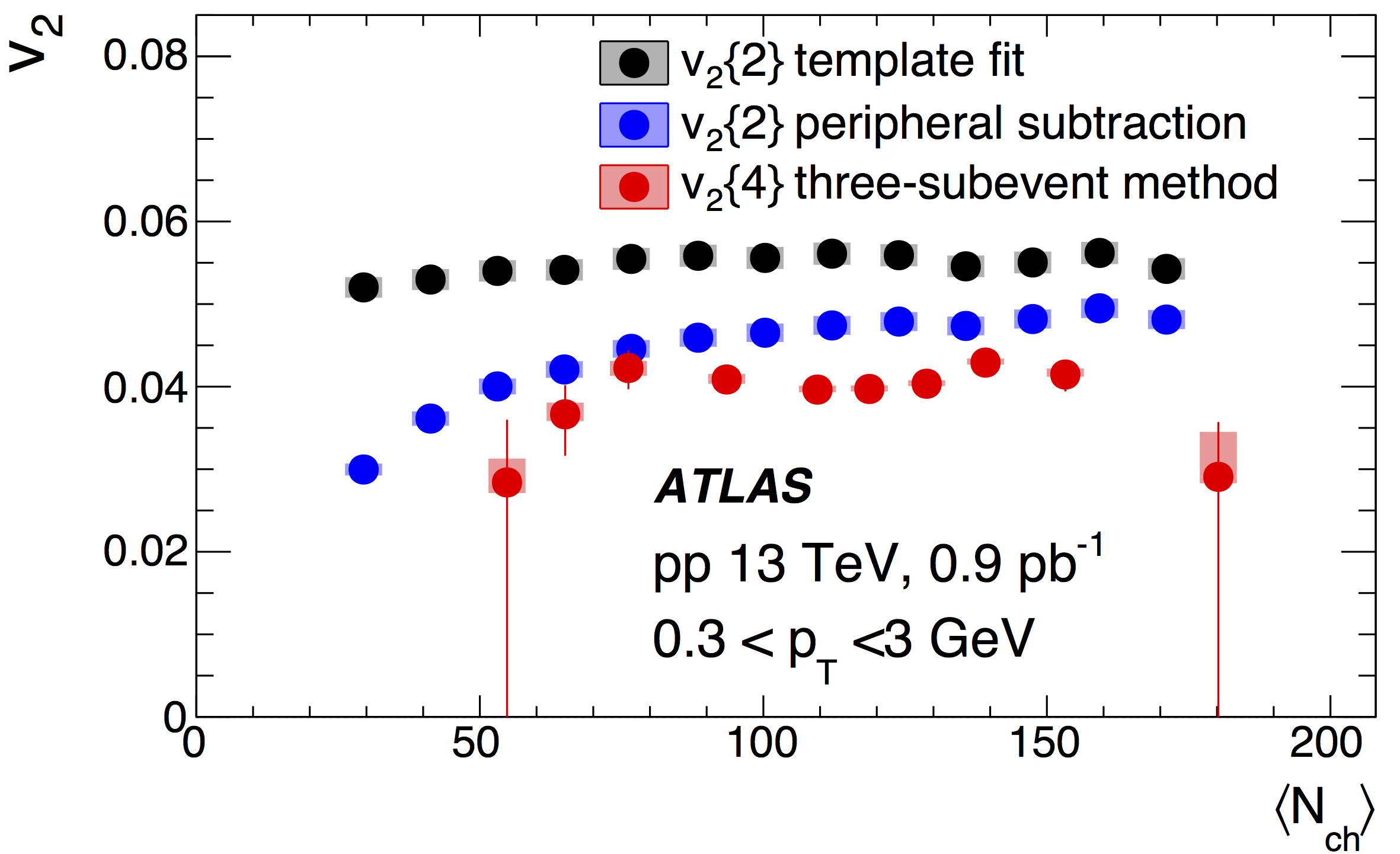
Figure 2 shows v2{4} as a function of the number of charged particles (Nch) which is characterised by charged particles in |η|<2.5 and 0.3< pT<5 GeV. The difference between v2{4} and v2{2} – the two-particle elliptic flow coefficient – is expected and is known to reflect the nature of event-by-event fluctuation of the ridge correlations (the latter must be smaller than the former). For the first time in proton-proton collisions, ATLAS measured a v2{4} “free” of non-collective correlations over a broad Nch range. In proton-ion collisions, the results extend the measurement reach of v2{4} to Nch as low as 20.
These results provide robust evidence that the multi-particle collective behaviour persists in small systems, even for small Nch. The lack of an observed Nch-dependence of v2{4} also indirectly supports the use of the template fit method, which is independent of Nch,, when extracting v2{2}. This new technique, and the new measurements, provide new insights on the nature of the ridge in small systems.
Links:
- Measurement of multi-particle azimuthal correlations in proton-proton, p+Pb and low-multiplicity Pb+Pb collisions with the ATLAS detector (EPJC 77 (2017) 428).
- Measurements of long-range azimuthal anisotropies and associated Fourier coefficients for proton-proton collisions at 5.02 and 13 TeV and p+Pb collisions at 5.02 TeV with the ATLAS detector (PRC 96 (2017) 024908).
- Measurement of multi-particle azimuthal correlations with the subevent cumulant method in proton-proton and p+Pb collisions with the ATLAS detector at the LHC (arXiv:1708.03559).
- See also the full lists of ATLAS Conference Notes and ATLAS Physics Papers.