ATLAS has been designed to detect rare events in high energy proton-proton collisions (see the last post “It’s all about the Lumi!”, by Jim). ATLAS ultimate goal is to measure events as rare as one in several thousand billions, but we are modest (for the time being) waiting for the luminosity to rise.

While over the last weeks priority has gone to LHC tuning in view of the luminosity increase, still some data have been taken in stable conditions and we have reached the sensitivity to see the production of W bosons (the charged mediator of the electroweak force). The predicted production rate of this particle is shown in the previous post (the sigma_W curve) indicating that one W is produced every few million ordinary collisions at 7 TeV.

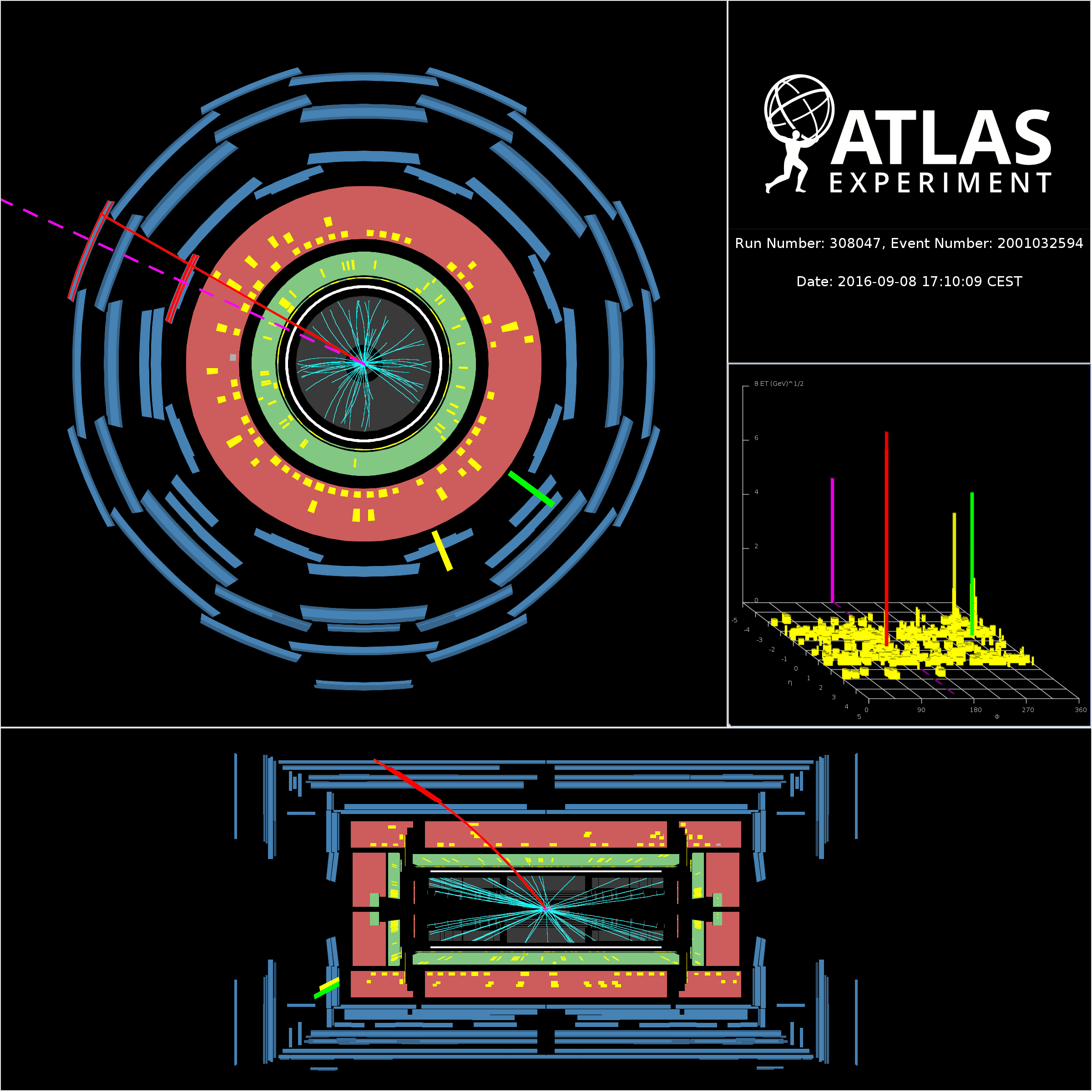
As the W is quite massive (~80 times heavier than the proton) and decays instantly in energetic particles it has a very peculiar signature which makes it pop-up out of the background of the ordinary collisions. This is particularly true when the two decay products are leptons. As the W is charged, one lepton should be charged (an electron, a muon or a tau) while the other should be neutral (a neutrino). An event where a W is produced should, for instance, contain a very energetic muon and a large missing energy recoiling against the muon. The neutrino can indeed travel kilometres in rock without interacting, it therefore “brings out of ATLAS” energy which can only be measured indirectly (as energy unbalance in the collision event or “missing energy”).

This pattern (an energetic muon and a missing energy recoiling against it) is exactly what has been seen in the event shown above, which is the first of few candidates W recorded by ATLAS. The era of the “high mass objects” in ATLAS has started!