Glossary
Adversarial training is a machine learning technique where one neural network (NN) is trained with one objective (usually signal-background separation) and one constraint, in order to make the NN output invariant with respect to some observable. This is achieved by training a second NN that attempts to predict the feature from the first NN output, and provides feedback to the first NN.
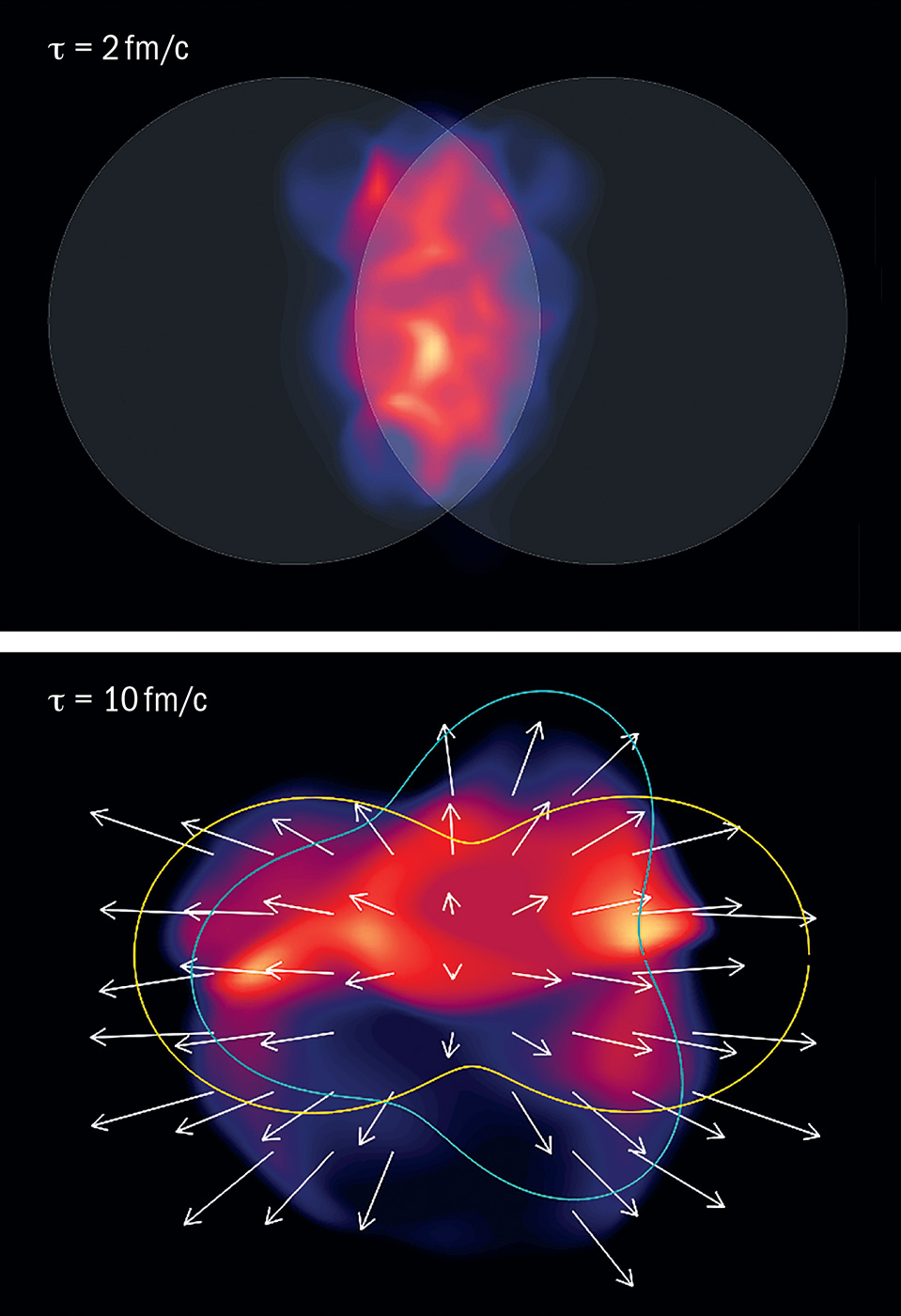
In heavy-ion collisions such as lead-on-lead, the produced Quark-Gluon Plasma (QGP) region may be spatially eccentric. This means it can be physically longer along one axis than another.
The high pressure at the centre of the QGP decreases to zero pressure in the vacuum outside the QGP region. The pressure gradient is therefore larger along the short axis than along the longer axis. This larger gradient leads to a stronger hydrodynamic flow for the particles emitted along the short axis than those along the long axis, increasing their momentum.
As a result, measurements of particles at fixed momentum find that there is a higher yield of particles in a quadrupole pattern along the short QGP axis. This is quantified as a second-order Fourier coefficient v2, known as the azimuthal momentum anisotropy.
The illustration shows the evolving energy density of the QGP created in a non-central collision. Pressure gradients act on the initial geometrical anisotropy to create a final velocity field (arrows), which may be decomposed into elliptic (yellow), triangular (teal) and higher order components. (Image: MUSIC/arXiv:1209.6330)
When searching for signs of new physics, physicists compare what they observe to what theories predict they will observe. The background is the set of results scientists expect to see. If an experiment sees more instances of a certain type of event (see “Excess”) than they expect to see as part of the background, it might be evidence of new physics.
When a particle decays, its mass before the decay can be calculated from the masses of its decay products. Researchers plot the masses of these decay products. If they originated from the particle being sought, they form a signal peak around the mass of the original particle. However, if they did not come from the original particle, they form a smooth distribution referred to as the combinatorial background.
Confidence Level (CL) is a statistical measure of the percentage of test results that can be expected to be within a specified range. For example, a Confidence Level of 95% means that the result of an action will probably meet expectations 95% of the time.
Particle physicists use the term cross section to describe the probability that two particles will collide and interact in a certain way. When proton beams cross in the Large Hadron Collider (LHC), many different processes can occur.
The cross section of a particular process depends on the type and energy of the colliding particles. Processes with larger cross sections occur more often than processes with small cross sections. At the LHC, certain particles such as W and Z bosons have large cross sections, so they will be observed more often. The production of a Higgs boson at the LHC has a much lower cross section, so is more difficult to produce.
Check out the cross section and luminosity cheat sheet to learn more.
A two dimensional plot used to describe the kinematics of a three-body decay. One typical usage is for the axes of the plot to be the squares of the invariant masses of two pairs of the decay products. If there are no angular correlations between the decay products then the distribution of these variables appears even.
Only 4.9% of the matter in the Universe is visible. The rest is known as dark matter (26.8%) and dark energy (68.3%). Finding out what dark matter consists of is a major challenge for modern science.
Particles decay into other particles over time. Decay channels are the possible transformations a particle can undergo as it decays. For example, the Higgs could decay into several different channels, such as two photons or two W bosons or two Z bosons. Physicists can calculate how long a particle should last and the ways it should decay. Knowing a particle’s decay channels can help physicists spot new particles created in ATLAS collisions, even if the particle decays before a detector can capture it. If experimentalists can’t see the particle itself, they can see the products of its decay.
When scientists observe more of a certain type of event than expected in a data plot, they call that an excess. Scientists measure the statistical significance (See “Standard deviation / Sigma”) of excesses to determine how certain they are that they result from new physics and not simply random fluctuations.
If a search for a particle reveals that it is statistically unlikely to exist with certain characteristics (e.g. a particular mass), a particle with those characteristics can be excluded. This narrows the search parameters within which the particle might be found. Establishing such exclusions is important in the search for undiscovered particles.
There are three families – or "generations" – of matter particles. Particles in different generations have similar properties but differ in mass from the lightest (first generation) to the heaviest (third generation). For example, the top quark (third generation) is about 80,000 times more massive than the up quark (first generation). For each of these particles, there exists a matching antiparticle with opposite charges.
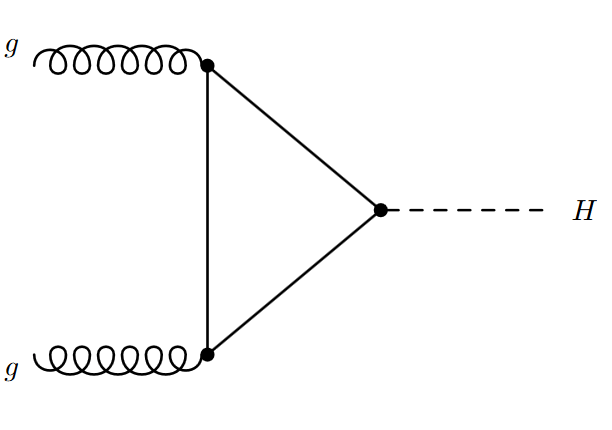
Two gluons, one from each of the incoming LHC protons, interact or “fuse” to create a particle, such as a Higgs boson. The figure shows a Feynman diagram illustrating the process.
In particle physics, the spin (S in the picture) is a fundamental property of particles, which is represented by a quantum number. The allowed values of S are: 0, 1/2, 1, 3/2, 2, etc. Particles with half-integer spin are known as fermions. Examples of fermions include: electrons, positrons, quarks that make up the protons and neutrons, and neutrinos. Particles with integer spin are known as bosons. Examples include the Higgs boson, the gluon, the photon, etc. Most of the known elementary bosons have spin=1. The exceptions are the Higgs boson, which has spin=0, and the graviton, expected to have spin=2.
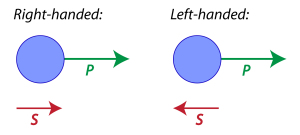
The spin of a particle is used to define its handedness: a particle is right-handed if the direction of its spin is the same as the direction of its motion. The particle is left-handed if the directions of spin and motion are opposite.
However, because the direction of motion depends on the reference system, if we take a reference system moving faster than the particle (something that is always possible for massive particles that cannot move at the speed of light), the particle will appear left-handed in this reference frame even if it was right-handed in another system.
The K meson (or kaon) is a composite particle composed of a strange quark and an up or down quark.
Leptoquarks are hypothetical particles that would allow leptons and quarks to transform into each other, giving a unified picture of the fundamental particles that form matter. Leptoquarks would be spin 0 (scalar) or spin 1 (vector) particles, and would interact via the strong force due to their colour charge.
Lorentz-contraction refers to the process of relativistic contracting of objects along the direction of motion. This is significant only for objects traveling at relativistic velocities.
Instantaneous luminosity measures how tightly particles are packed into a given space, such as the LHC's proton beam. A higher luminosity means a greater likelihood particles will collide and result in a desired interaction. This can be achieved by packing more particles in the beam, or by focusing the beam more tightly.
Integrated luminosity, on the other hand, considers the total number of events during a period of data-taking. The ATLAS Experiment recorded 147 inverse femtobarns of data during the LHC's 13 TeV run from 2015-2018, which equates to about 16 million billion proton–proton collisions!
Check out the cross section and luminosity cheat sheet to learn more.
Particle physicists use the word "mass" to refer to the quantity (sometimes called "rest mass") which is proportional to the inertia of the particle when it is at rest. This is the "m" both in Newton's second law of motion, F=ma, and in Einstein's equation, E=mc2 (in which E must be interpreted as the energy of the particle at rest). When a particle decays and hence no longer exists, its mass before the decay can be calculated from the energies and momenta of the decay products. The inferred value of the mass is independent of the reference frame in which the energies and momenta are measured, so that that the mass called "invariant". The concept is frequently generalized, so that for any set of particles (e.g., two leptons emerging from a collision), one can apply the same formulas to obtain an "invariant mass" (also called the “effective mass”) of the set.
One of the important statistical tools in particle physics is to create a histogram of the invariant mass of a particle or a group of particles (thought to originate from the decay of something interesting) versus the frequency with which that particular mass was recorded. This plot is known as a mass spectrum, and is used to signify the presence of new particles and to establish their masses.
In particle physics, some phenomena can be best described by two separate quantum mechanical states with respect to some underlying symmetry. If the observed state is rotated within this underlying symmetry, it is called a "mixed state". There is thus a probability to observe one or the other underlying quantum mechanical state. This probability is determined by the rotation angle within this coordinate system, called the "mixing angle".
Scientists construct and develop 'models' to describe a scientific theory in the context of related phenomena. In general, a model is based on a theory (a set of hypotheses), acting on a set of parameters obtained from actual experimental data and/or from observations. Computer simulations may sometimes be used to test the reliability of a model. If it was found to be reasonably reliable, the simulation can even be used to predict what would happen if the initial parameters were different.
A neural network is a machine learning algorithm that receives as input a number of variables or features, and finds the best combination of those features to predict an output. The output can be a simple categorisation (e.g. does this event contain a Higgs boson?) or predicting a quantity (e.g. what was the momentum of the particle that left these energy deposits in the detector). A deep neural network is a type of neural network that uses multiple layers to progressively compute more complex features from the raw input in order to achieve a more accurate output.
The p-value is the probability (ranging from 0 to 1) that the results observed could have occurred by chance, if the tested theory has no impact on the study.
Check out the Statistical Significance cheat sheet to learn more.
The 3D position space is thought to be along 3 axes, such that a set of three numbers (x,y, and z) can fully describe the location of an object. However, in a collision event, there are many other observable features that are crucial for adequately describing the particles that are formed, such as the angles and momenta of the outgoing particles or the quantity of each type of particle created. These observable features can uniquely define a single collision event in a high-dimensional "phase space”. Therefore, phase space is a good approach to picture particle collisions since different types of processes will be found in different sections of it.
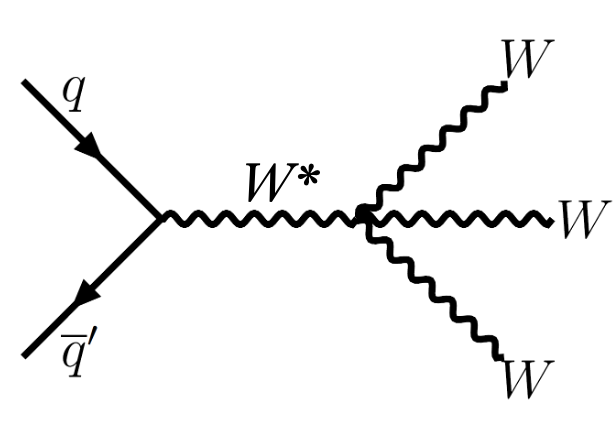
When four gauge bosons interact with each other, the strength of this interaction is known as the "quartic gauge boson coupling". This parameter is represented in Feynman diagrams by a vertex where four gauge boson lines meet.
The figure shows quark-quark interaction, where one virtual W boson decays into three W bosons; the convergence of the interaction lines is the “quartic gauge boson coupling”.
Also known as "matter-parity". In many Supersymmetry (SUSY) models, R-parity ensures that protons – and hence all of the atoms in the universe – are unable to decay to other particles quickly by exchanging SUSY particles. Though this can also be prevented in models without R-parity conservation, introducing R-parity is often considered the simplest possibility.
The R-parity (Rp) of a particle is defined by:
Rp = (−1)3(B−L)+2s
where B is baryon number, L is lepton number, and s is spin. R-parity has a value of (+1) for Standard Model particles and (-1) for their superpartners.
Conservation of R-parity prevents proton decay via exchange of a superpartner into a positron and a neutral pion. Conservation of R-parity also prevents the decay of the lightest superpartner into standard model particles, and thus the lightest superpartner becomes an appealing candidate for dark matter.
While conservation of R-parity accomplishes its purpose of preventing proton decay, other choices are possible. Extending the Standard Model with a new gauge symmetry with charge (B–L) would give a natural way to suppress unwanted baryon- and lepton-number-violating interactions, and would allow the lightest superpartner to decay.
Rapidity is used to express angles with respect to the axis of the colliding beams, which are well-defined for particles travelling close to the speed of light. When particles travel at high velocities, angles defined in more familiar ways can grow or shrink, making discussion of these quantities difficult. Rapidity has the value 0 for particle trajectories that are perpendicular to the beam, and positive or negative values for those at an angle to the beam.
Pseudorapidity is an approximation to Rapidity. This quantity is sometimes used instead of Rapidity as it is easily calculated from the cartesian angle between the particle direction above or below the beam line and has a direct relationship with detector components. This quantity is precisely equivalent to Rapidity for massless particles.
Measure of the accuracy of a detector measurement, e.g. of energy or spatial position.
The number of observed events divided by the number of expected events is called the signal strength or mu (μ). The closer the value of μ is to one, the more consistent is the observation to the Standard Model.
Simplified template cross sections (STXS) are an approach to categorise the Higgs-boson candidate events according to the properties associated with the Higgs production mode. This allows physicists to characterise the Higgs boson independently of its decay channel.
Spin is the intrinsic angular momentum of an elementary particle, measured in units of the reduced Planck’s constant ħ. In quantum field theory, the spin of a particle is related to its behaviour. For example, particles with integer spin (0, 1, 2…) are called bosons, and can occupy the same quantum state at the same time. In contrast, particles with half-integer spin (1/2, 3/2, 5/2…) cannot. The known elementary constituents of matter (electron, quarks, neutrinos…) are spin 1/2 particles, whereas the particles (photon, W/Z, gluon) which mediate the known interactions (respectively electromagnetic, weak, strong) are spin 1 particles.
The Higgs boson has spin 0 (it is a so-called “scalar” boson) and positive parity as predicted by the Standard Model. It is the only elementary scalar particle to be observed in nature.
A standard deviation is a measure of how unusual a set of data is if a hypothesis is true. Physicists express standard deviations in units called sigma, σ. The higher the number of sigma, the more incompatible the data are with the hypothesis.
If the data are incompatible enough with a hypothesis that says the experiment will find only background, that could constitute a discovery. Typically, the more unexpected or important a discovery, the greater the number of sigma physicists will require to be fully convinced. Five sigma significance is traditionally required to claim a discovery of a new particle; this was the threshold passed by the Higgs boson when its discovery was announced on 4 July 2012.
Check out the Statistical Significance cheat sheet to learn more.
The blueprint for a sub-detector system.
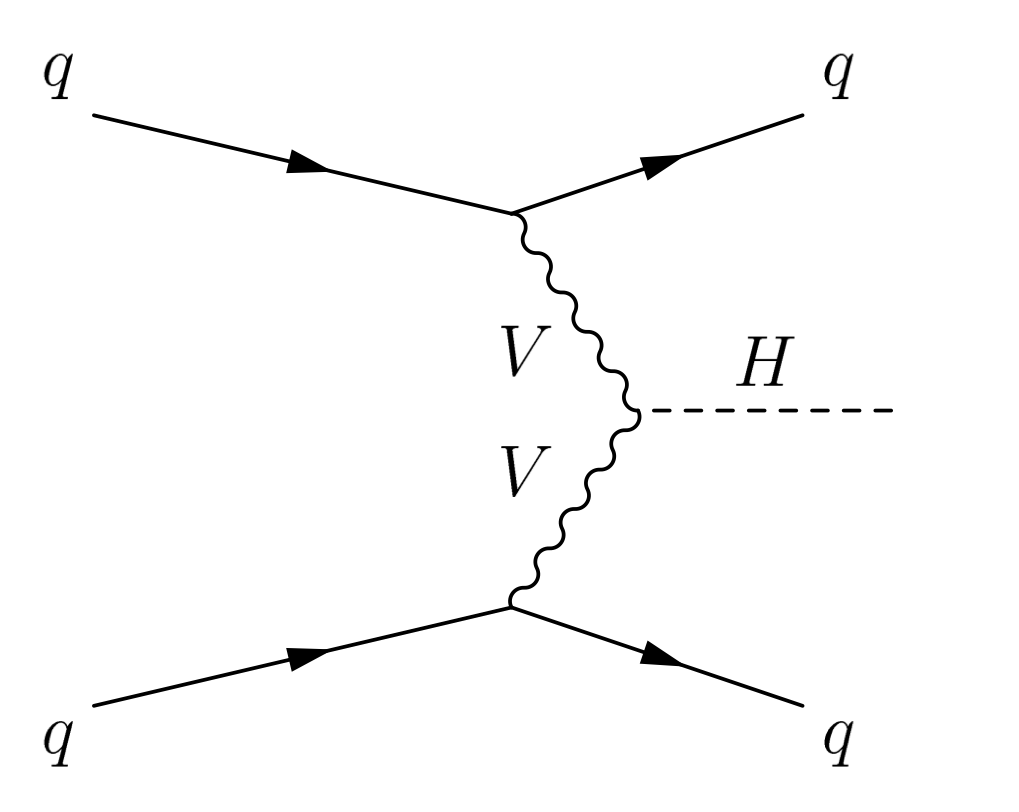
A quark from each of the incoming LHC protons radiates off a heavy vector boson (V), which are either W or Z bosons. These bosons interact or “fuse” to produce a particle, such as a Higgs boson. The initial quarks that first radiated the vector bosons are deflected only slightly and travel roughly along their initial directions. They are then detected as particle "jets" in the different hemispheres of the detector. The figure shows a Feynman diagram of this process.