5 fundamental parameters from top quark decay
3 August 2017 | By
For many physicists, discovering “new physics” means bringing to light a new particle. Another path to discovery lies in carefully measuring the properties of known particles and the interactions between them. The ATLAS experiment has now released new results on the top quark's interaction with the charged intermediate vector boson.
While the Higgs boson, which escaped observation until as recently as 2012, is certainly the most intriguing elementary particle, the top quark is arguably second. Heavier than even the Higgs boson, the top quark packs as much mass as a gold nucleus into a single point like constituent. Precise measurements of the top quark have taken a great leap forward at the Large Hadron Collider (LHC), where the production rate is high and the backgrounds are low.
In the recent paper, the ATLAS collaboration presents results obtained from decays of polarised top quarks. The polarisation occurs when top quarks are produced singly through the parity-violating weak interaction, rather than in pairs through the parity-conserving strong interaction. Singly-produced top quarks have only recently become an important tool for discovery.
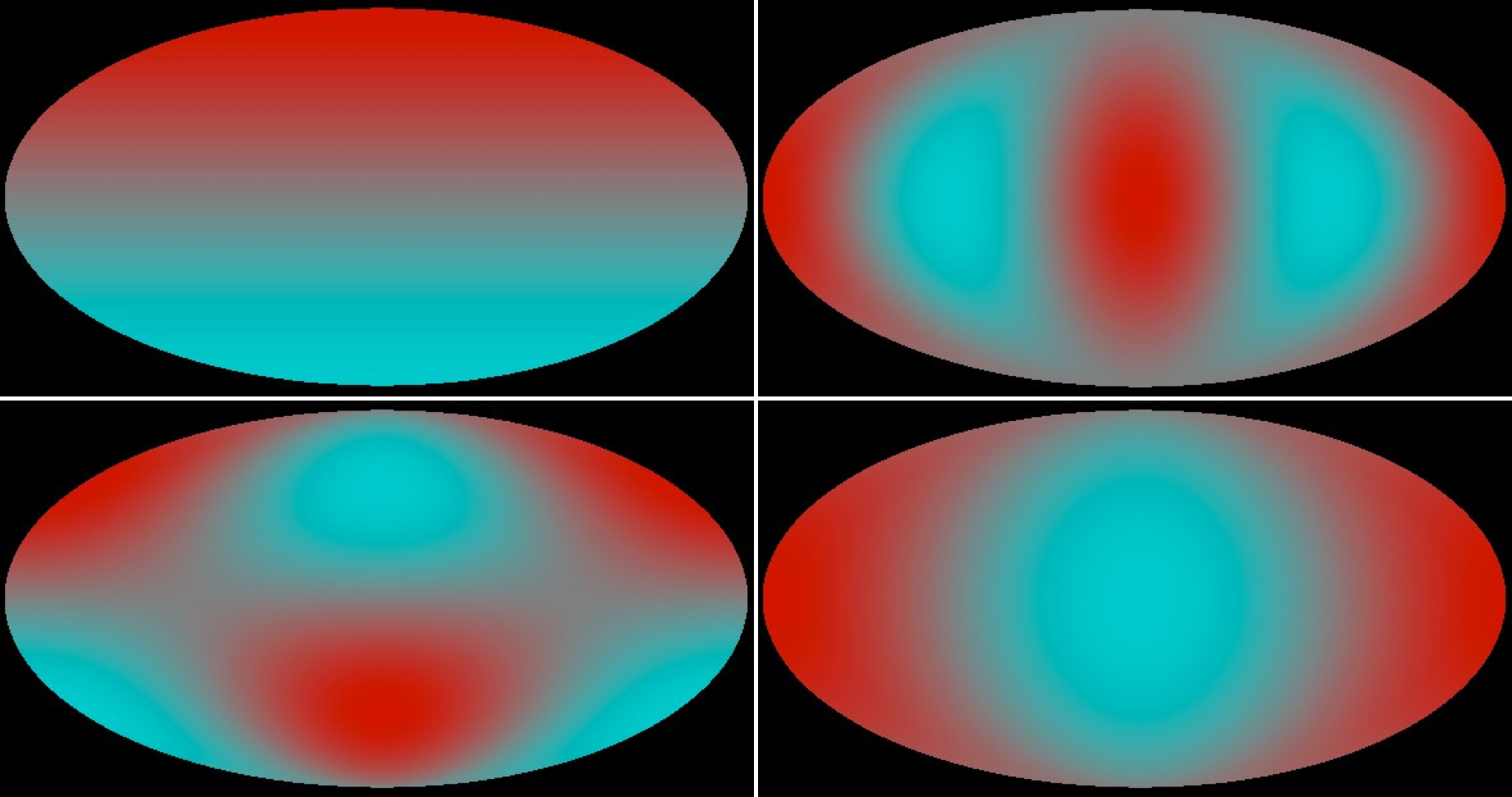
Nine distinct decay patterns, examples of which are shown in Figure 1, can be discerned in these decays, similar to antennae patterns. These patterns depend upon five fundamental constants (called f1, f1+,f0+,δ-, and P) governing the interaction between the top, its partner the bottom quark, and the charged weak boson (W±). Current understanding of physics holds that the top quark couplings should be “left-handed” like those of the other quarks, and that they should be identical between the top quarks and its antiparticle, the top antiquark. The new measurements put that understanding to the test.
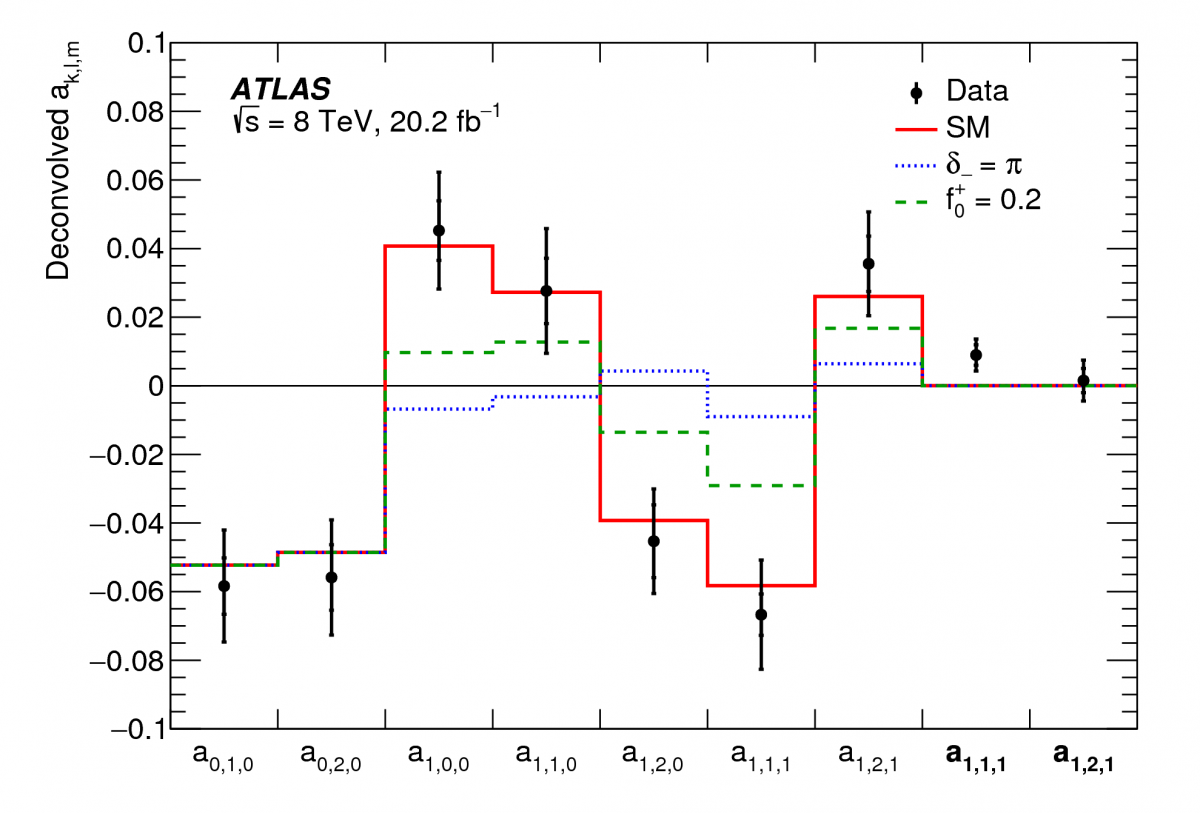
By studying the full multidimensional decay patterns, ATLAS measures many properties of the top-bottom-W interaction at the same time and without some of the assumptions that have been made in the past. The analysis is known for both its complexity and its power. Results are shown in Figure 2. Five fundamental constants are determined from the decay. The fourth one, δ–, quantifies the matter-antimatter asymmetry in top quark decays. It is consistent with zero and consistent with the current understanding of fundamental physics. Shocking? Maybe – but physicists are slowly getting used to the idea that the Standard Model is an excellent description of nature.
The analysis uses proton–proton collisions at 8 TeV, data collected at the LHC in 2012. Investigators are now applying even more refined techniques to collisions at a higher centre-of-mass energy of 13 TeV now being collected at CERN. Future measurements at higher precision may finally observe deviations from the Standard Model.
Links:
- Analysis of the Wtb vertex from the measurement of triple-differential angular decay rates of single top quarks produced in the t-channel at s√ = 8 TeV with the ATLAS detector (arXiv:1707.05393).
- EPS 2017 presentation by Susana Cabrera Urban: Anomalous couplings in single top and searches for rare top quark couplings with the ATLAS detector
- See also the full lists of ATLAS Conference Notes and ATLAS Physics Papers.