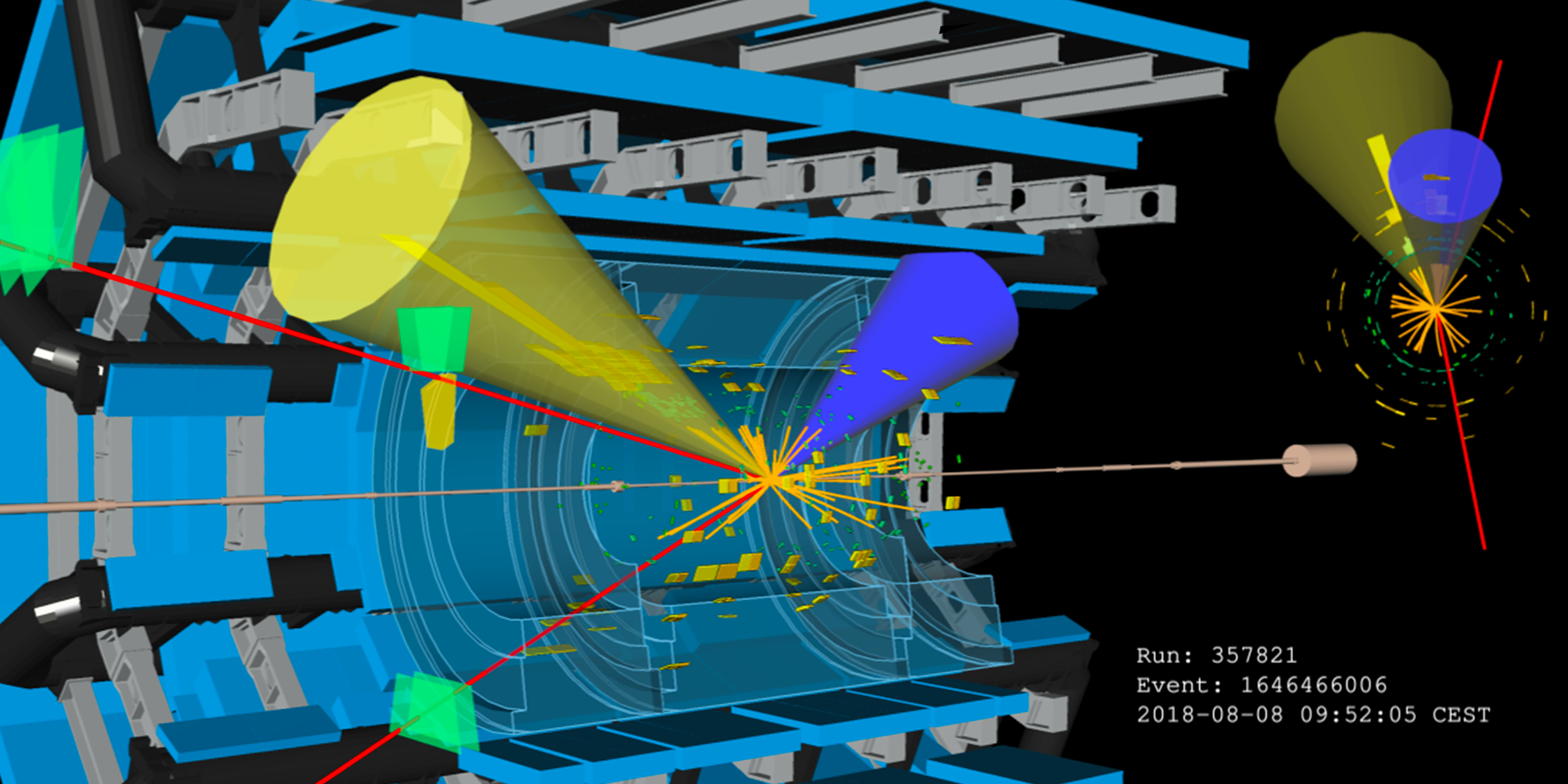
Broken symmetry: searches for supersymmetry at the LHC
8 December 2017 | By
The close connection between symmetry and the laws of physics is one of the greatest scientific insights to develop in the twentieth century. Noether’s Theorem – named after the German mathematician Emmy Noether, who proved the theorem in 1915 – drew the first connection between the symmetries of space-time and the conservation laws of physics. It posed, for example, that the symmetry of the laws of physics under time translation result in the conservation of energy. In other words, they are the same today as they were a billion years ago. Symmetry under spatial translation, meanwhile, results in the conservation of momentum.
Yet another symmetry, known as “gauge symmetry”, is also observed. Consider a bird sitting on a live wire. Why does it not die? Because absolute voltages are meaningless: the laws of physics are invariant as to what we arbitrarily call “ground”. Only differences in voltages between objects are important, as they lead to a current between those objects. As long as our bird does not experience voltage differences, it is safe.
A similar concept is operational in the quantum world. In particle physics, gauge symmetry posits an invariance of the laws of physics under the “rotation” of quantum fields in an abstract mathematical space. The implications are staggering. Gauge symmetry gives rise to a unifying mathematical structure, known as the “Standard Model”, that describes all matter and (so far) three of the four fundamental forces in the Universe.[1] As a result, nuclear forces – which power the Sun, and give rise to radioactive decay and the promise of unlimited energy through nuclear fusion – can be described in the same mathematical framework as electromagnetic forces – underlying radio communications and most chemistry. The Standard Model clearly stands out as one of the crowning intellectual achievements of the twentieth century.
And yet, there is an underlying paradox. Our world is visibly not symmetric; it is clumpy and irregular. Even at the subatomic scale, where one might imagine things to be more uniform, there are profound asymmetries. For example, the weak nuclear force acts only over subatomic distances, while the effects of electromagnetism can be felt at macroscopic scales.
Here we face another of the most profound insights into the structure of physical law: the notion of broken symmetry. Condensed matter physicist Phillip Anderson is usually credited with coming up with the first ideas on how an asymmetric world might arise from underlying symmetric laws of physics. In a beautiful example of cross-disciplinary physics, these ideas were then taken to the subatomic realm by Yoichiro Nambu in the early 1960’s. Three independent efforts by Robert Brout and Francois Englert in Brussels; Gerald Guralnik, Carl Hagen and Tom Kibble at Imperial College in London; and Peter Higgs at the University of Edinburgh, would lead to a concrete model known as the Brout-Englert-Higgs Mechanism.[2] It posits a Higgs field that fills the entire Universe, with localised excitations of this field, namely the Higgs boson.
The different interactions between the Higgs field (that fills empty space), and the carriers of the weak force (W/Z bosons) and electromagnetic force (photons), break the symmetry inherent in the unified description of these two vastly different forces. The W/Z bosons acquire mass through their interaction with the Higgs field, making them short-range force-carriers, while the photon remains massless, allowing the electromagnetic force to have infinite range. The energy scale of this unified description, where weak and electromagnetic forces have similar strength, defines the so-called electroweak scale. This practical application of symmetry breaking was put forward as a “toy model", but was not expected to be found in Nature in this simple form.
A fundamental problem (known today as the “hierarchy problem”) was first noticed by Kenneth Wilson in the early 1970’s. The Higgs boson, which “gives mass” to all fundamental particles, gives itself mass. However, this mass turns out to be theoretically unstable and, in this model, is around a factor of 1016 larger than the electroweak scale. This difference was widely considered “unnatural”: a problem asking for a solution.
The Standard Model clearly stands out as one of the crowning intellectual achievements of the twentieth century. And yet, there is an underlying paradox. Our world is visibly not symmetric; it is clumpy and irregular.
The 1960’s through the mid 1980’s were truly a golden age for particle physics, with remarkably fruitful interactions between experimental and theoretical advances that led to the firm establishment of gauge symmetry (and its breaking) as fundamental, unifying principles. Yet, some important issues remained unresolved, most notably the experimental discovery of the exact mechanism for breaking electroweak symmetry, and the theoretical hierarchy problem.
The 1970’s saw the arrival of a radical new symmetry principle: “supersymmetry”, or SUSY for short. This remarkable new idea was simultaneously and independently developed on both sides of the Iron Curtain. How it went from a mathematical curiosity (largely outside the mainstream) to dominating theoretical (and to a large extent, experimental) particle physics is a fascinating story… one much too long to go into here!
SUSY extends the symmetries of space and time into the quantum domain, connecting the purely quantum mechanical property of “spin” to classical macroscopic quantities like space and time. By imposing certain conditions of “locality”, you can obtain General Relativity, Einstein’s theory of gravity. Is this starting to sound like quantum gravity? Then you’ll understand some of the excitement!
SUSY puts bosons (force carriers) and fermions (matter) on a symmetric footing, unifying the description of forces with that of matter. In practical terms for experimentalists, SUSY doubles the number of fundamental particles, with a SUSY “partner” particle for each Standard Model particle.[3] Under supersymmetry, the strengths of the fundamental forces become the same (unified) at short distances. Supersymmetry naturally gives the Higgs boson the property that allows it to break the (electroweak) symmetry between the weak and electromagnetic forces. Supersymmetry naturally gives rise to a particle that fits all the characteristics of the dark matter in the Universe. And, as if that were not enough, supersymmetry provides a natural solution to the hierarchy problem: the unstable terms in the calculation of the Higgs boson mass, arising from interactions of the Higgs boson with Standard Model particles, are canceled by similar terms, of opposite sign, arising from the SUSY partners.
Understanding the breaking of electroweak symmetry (from the Higgs boson, or some other mechanism?) and the search for a solution to the hierarchy problem (supersymmetry?) have arguably been two of the primary drivers of research in particle physics since the 1980’s. At CERN, the Super Proton Synchrotron (SPS) and Large Electron-Positron (LEP) colliders elucidated the nature of the weak interaction, but did not find the Higgs boson nor SUSY. In the United States, plans were made for a Superconducting Super Collider (SSC) to find the Higgs boson. The cancellation of this project in the mid 90’s was a tremendous shock to the “big science” community. A smaller machine at Fermilab in Chicago, the Tevatron, that operated between 1983 and 2011 was very successful. It discovered the top quark and a significant number of other phenomena, but found neither the Higgs boson nor SUSY.
With these machines in mind, the completion of the Large Hadron Collider (LHC) at CERN was greeted with high hopes in 2007.
SUSY extends the symmetries of space and time into the quantum domain, connecting the purely quantum mechanical property of “spin” to classical macroscopic quantities like space and time.
The LHC is an enormous facility. It is a circular accelerator, 27 kilometres in circumference, straddling the Swiss-French border on the outskirts of Geneva. Four experiments are situated around the LHC ring, two of which (ATLAS and CMS) are general-purpose facilities. They study the collisions of protons, accelerated by the LHC to 99. 999999% of the speed of light, which, owing to special relativity, increases their rest mass by a factor of about 7000. These experiments can be considered giant cameras, taking 40 million “photos” per second, and generating a few petabytes of data per year.
The LHC has two advantages over its predecessors: first, it collides protons with the highest energy ever achieved; second, it records a much larger number of collisions. Furthermore, the ATLAS and CMS detectors are truly state-of-the-art.
Data-taking began in earnest in 2009, with the volume of data growing quickly as the detectors worked above expectation. Initial searches for supersymmetric particles focused on particles that could be discovered with relatively little data: the SUSY partners of quarks and gluons, known as “squarks” and “gluinos”. Their production mechanisms benefit from the high collision-energy and, for these particles in particular, the LHC opened up a completely new domain. The production rate of squarks and gluinos, encoded in a quantity called “cross-section”, is well calculated, with only their unknown masses as free parameters. Squarks and gluinos are expected to be unstable and decay into the quarks and gluons of the Standard Model. But they are accompanied, in the most popular SUSY model, by a stable and very weakly interacting particle, called the “Lightest Supersymmetric Particle” or LSP.
Due to their very weak interactions, LSPs will typically leave no trace in ATLAS and CMS detectors, just as the well-known neutrinos do. However, their presence can be deduced with some detective work: they would leave an imbalance in the distribution of the energy of the visible particles in the detector, in apparent contradiction to the laws of conservation of momentum. Of course, these laws are respected by Nature, and allow us to play the opposite game: to reconstruct any LSPs that may occur in the event. The signature of heavy squarks and gluinos would then be a surplus of collision events with a high number of very energetic jets (arising from the quarks and gluons in the decay of the heavy squarks or gluinos) and a significant amount of missing energy, carried away by the LSPs.
Before the LHC started, the concept of SUSY as a solution to the hierarchy problem gave rise to certain expectations on the masses of the SUSY particles. After all, it was only if the masses of the Standard Model particles and their SUSY partners do not differ too much that SUSY would provide a solution. However, what “do not differ too much” means exactly is hotly debated. Expectations were that the carriers of the weak force (the W and Z bosons) and their SUSY partners would have roughly the same mass. Partners of the top quark were thought to be perhaps as much as five times heavier than these weak-force partners. And the partner of the gluon (the carrier of the strong nuclear force) could be ten times heavier.
The hoped-for surplus of events described above was not observed in the initial run of the LHC, nor has it yet been seen in LHC Run 2 with increased collision energy. Given this absence, constraints have been set on the production cross-section of squarks and gluinos, and from these, limits on the squark and gluino masses have been derived. These constraints are now very tight: it is unlikely that gluinos exist with a mass below about 2000 GeV (more than 20 times the mass of the weak force carriers), for example.
In parallel to these first SUSY searches, ATLAS and CMS carried out the search for the Higgs boson in full force, with exciting results. The first hints of a signal appeared in late 2011; these were tentative, but having two independent experiments showing the same signs gave credence to the notion that discovery was at hand. Full confirmation came half a year later, leading the Director General of CERN to famously declare, “I think we have it” to a packed auditorium (and thousands watching online) which included Englert, Higgs, Hagen and Guralnik.
Since then, refined measurements seem to confirm with higher and higher accuracy the simple picture of the relatively light Higgs boson, something that was initially disparaged as a mere “toy model”. These results only enforced the uneasiness that particle physicists feel about the hierarchy problem. We came to realise, however, that not all squarks are equal in their importance to solve the hierarchy problem: the largest contributions to the unstable terms in the Higgs mass calculation arise from the top quark, and must be balanced by its SUSY partner, the scalar top quark or “stop”.
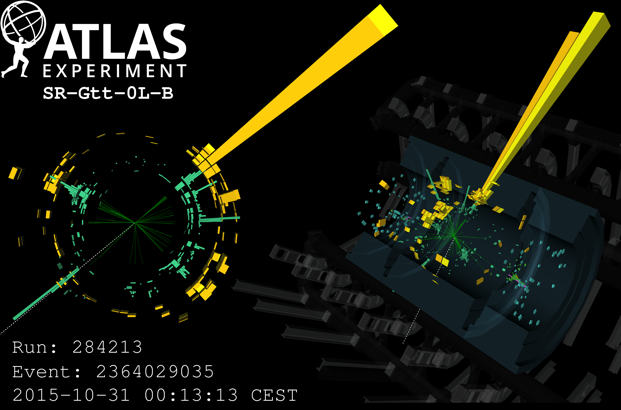
As the decays of the stop differ in a number of respects from those of other squarks, generic searches for squarks and gluinos would not be very effective for stops. So with renewed vigour, dedicated searches for stop quarks were designed and applied to the data. These searches are complicated by the fact that the stop can decay in a number of different ways, and that the importance of each decay mode is strongly influenced by the stop mass, as well as by the unknown masses of other SUSY particles. Despite the large cross-section of a relatively light stop (with a mass close to the top quark mass), such particles are quite difficult to spot due to presence of very large Standard Model background signals.
The newly-designed dedicated searches also came out empty, allowing us to constrain the properties of the stop. If it exists, its mass should exceed approximately 1000 GeV, at least a factor of 10 above the masses of the weak force carriers.
But there’s a catch. The searches described above are most effective when the LSP is light, but not so much when the LSP is heavy. However, the LSP mass is also a free and unpredicted parameter. If the LSP is heavy, the amount of missing energy reconstructed in the detectors is rather small, and difficult to separate from the background. Recognising this, ATLAS and CMS designed dedicated searches for SUSY events accompanied by a very energetic jet or photon radiated by one of the protons just before collision. In such events, the SUSY particles will get a “kick” that increases their visible energy. Indeed, this improved the sensitivity of the searches involving heavy LSPs, but all limits on squarks – including stops – and gluinos are still rather weak when the LSP mass is high. It is important to realise this “fine print” whenever limits on SUSY are quoted.
The properties of the LSP also correspond very well with those predicted for dark matter particles. This is important motivation for the search for direct production of the class of SUSY particles of which the LSP is most likely a member: charginos and neutralinos, the supersymmetric partners of the gauge bosons of the weak force and of the Higgs boson. This is significantly more difficult than the search for squarks or gluinos. Charginos and neutralinos are produced with rather small cross-sections. Thus, any experimental search for them requires a lot of data. Such data has only recently become available, now that we have had a few years of LHC runs. Furthermore, the properties of charginos and neutralinos, including the production cross-sections and decay modes, are subject to much more uncertainty than those of squarks and gluinos. Searching for them is most effective in final states with low backgrounds, involving two or more charged leptons, and some missing energy.
Recent results have also shown no surplus of such events, setting lower limits on chargino and neutralino masses typically of a few hundred GeV. However, these searches cover far from all the options and are also limited by the size of the current LHC dataset. Therefore, they are still very much at the forefront of current SUSY research.
When Einstein was asked how he would react if his theory of General Relativity was not confirmed by experiment, he reportedly replied: “the Lord has missed a most marvellous opportunity”.
The beautiful theoretical ideas underlying supersymmetry have not been seen in Nature – at least, not in the simplest form we expected. When Einstein was asked how he would react if his theory of General Relativity was not confirmed by experiment, he reportedly replied: “the Lord has missed a most marvellous opportunity”. To many, supersymmetry is a similarly beautiful “opportunity” that still cannot be simply discarded. Supporters continue to hope that supersymmetry will eventually be discovered at the LHC, though perhaps in a different form than initially expected. It is a cruel irony that sometimes toy models turn out to be correct and beautiful ideas fall by the wayside. Ultimately, measurements of Nature decide what is fundamental.
There are still windows where supersymmetry (or some other solution to the hierarchy problem) might appear. These windows are narrowing, but if the experience of the Higgs boson is any guide, the last window is sometimes where things finally show up! In the history of particle physics, there are stories (perhaps apocryphal) of giving up too soon only to be scooped by a later experiment. Some think the window is in fact not that narrow; supersymmetry is also a broken symmetry, after all, and our belief in a narrowing window of discovery is based on certain prejudices about supersymmetry breaking.
However, it is clear where the search for supersymmetry will be headed next. Over the coming years, experiments will be in pursuit of SUSY particles with small cross-sections, such as charginos and neutralinos; SUSY particles that do not decay immediately after production, but instead have a finite lifetime leading to particular, and rather special, final states; final states with heavy LSPs; and final states without a LSP, with little or no missing energy.
Though the experimental search for supersymmetry has come up empty-handed so far, it has left a permanent mark on our field. Clever, sophisticated techniques and observables have been devised to optimally separate signal from background, and which have applications beyond the SUSY search. Furthermore, the interpretation of the results no longer takes place in a limited set of highly constrained models of supersymmetry, but rather in simplified models that are much more general and less theory driven. Combined with the publication of experimental information, such as efficiencies and backgrounds, this allows our published results to be reinterpreted in different models by theoretical physicists.
It is also important to continue studying the Higgs boson in ever more detail; it may provide a hint that leads to deeper understanding. It is a unique beast; there is no other particle like it. No field other than the Higgs field fills the entire Universe with a non-zero average value, and then gives the Universe a lower energy than if the Universe were empty. Some (mostly theorists) have punted on the hierarchy problem, claiming that it is “just so” that the Higgs boson has such an un-natural mass. This is not the first time that things turn out “just so”. In the 16th century, elaborate models were developed to explain why the planets in our solar system have the spacing that they do. The recent solar eclipse in the United States revived the question of why the moon and Sun cover almost exactly the same area in the sky. We now understand that there is nothing special about these spacings – there are many planetary systems and ours is “just so”. Could it be that there are many universes and we happen to live in the one that is “just so”? This is an active area of research, but it strikes many as a dead-end because it seems impossible to verify experimentally.
Though the experimental search for supersymmetry has come up empty-handed so far, it has left a permanent mark on High-Energy Physics.
While the LHC continues to perform at unprecedented levels, both the ATLAS and CMS experiments are preparing to be upgraded with even more sophisticated technology. The promise of ever increasing datasets of higher and higher quality is a dream for any experimentalist. Yet there hangs over the community a certain shadow. The breaking of symmetries turns out to be central to realization of the laws of Nature as we know them. The breaking of electroweak symmetry has been confirmed by experiments to be described very well by the Standard Model. The expectation, however, of a somewhat (but not too strongly) broken supersymmetry, that could solve some of the unanswered questions left behind by the Standard Model, has not yet been confirmed.
There is still plenty of opportunity to find some of these answers in the upcoming data. But we may also need to come to terms with a different picture of Nature: one with the absence of such answers at the LHC scale. Perhaps it is our over-simplistic view that is broken, and not just SUSY. Perhaps Nature is telling us that we are looking at the problems of the Standard Model in the wrong way. History has shown that times such as these are precious, since they may well contain the seeds of true progress.
About the authors
Paul de Jong is professor in experimental particle physics at the University of Amsterdam and senior scientist at the Dutch National Institute for Subatomic Physics (Nikhef). George Redlinger is scientist at the Brookhaven National Laboratory, USA. Both are members of the ATLAS experiment at CERN’s Large Hadron Collider and have been mining ATLAS data for signs of supersymmetry for many years.
[1] The four forces are: gravity, electromagnetism and the strong and weak nuclear forces. The strong force holds atomic nuclei together while the weak force is responsible for radioactive decay. The latter three forces can be described in terms of a unified “gauge” theory, commonly known as the Standard Model. To date, only the gravitational force remains outside this unified framework. A quantum theory of gravity remains as the Holy Grail of fundamental physics.
[2] Some physicists have advocated using the (admittedly awkward) nomenclature, the ABEHGHK mechanism/field/boson, after the afore-mentioned seven physicists who played the most prominent role in developing this powerful idea. We follow common practice here and use the shortened form.
[3] This would not be the first time the cast of fundamental particles is doubled. The experimental discovery in 1922 of what was eventually to be called “spin” was perhaps the first doubling, with “spin up” and “spin down” particles. Spin arises naturally in relativistic quantum mechanics formulated in 1928 by Paul Dirac; the theory also predicted the existence of antiparticles. Experimental observation of the first antiparticle (the anti-electron, or positron) by Carl Anderson in 1932, the further development of quantum field theory and the observation of many other antiparticles confirmed this second doubling of the number of fundamental particles. The SUSY partners would carry the same quantum numbers as their known counterparts, except for their spin that differs by half a unit. Thus, the partners of matter particles have the spin of force carriers and vice versa.