Hunting for new physics with boosted bosons

6 August 2016 | By

Figure 1: One of the highest dijet mass events in the search looking for a pair of hadronically decaying vector bosons coming from a new heavy resonance. Within the energy deposited in the calorimeters (green and yellow bars), as in the reconstructed tracks (orange lines), two clear groups are seen. The new techniques used to identify hadronic decaying bosons are utilising exactly these features to maximize the search sensitivity. (Image: ATLAS Experiment/CERN)

The Standard Model is a tremendously successful theory that describes our best understanding of elementary particles and their interactions, and even predicted the existence of the Higgs Boson. It does not however explain ~95% of the known universe – including dark matter and dark energy – and does not include a description of gravity. There are many theories that address these issues by expanding upon and modifying the Standard Model. As experimental physicists, we have no preferred model. This leads us to push our current knowledge to new extremes by testing all the viable extensions to the Standard Model.

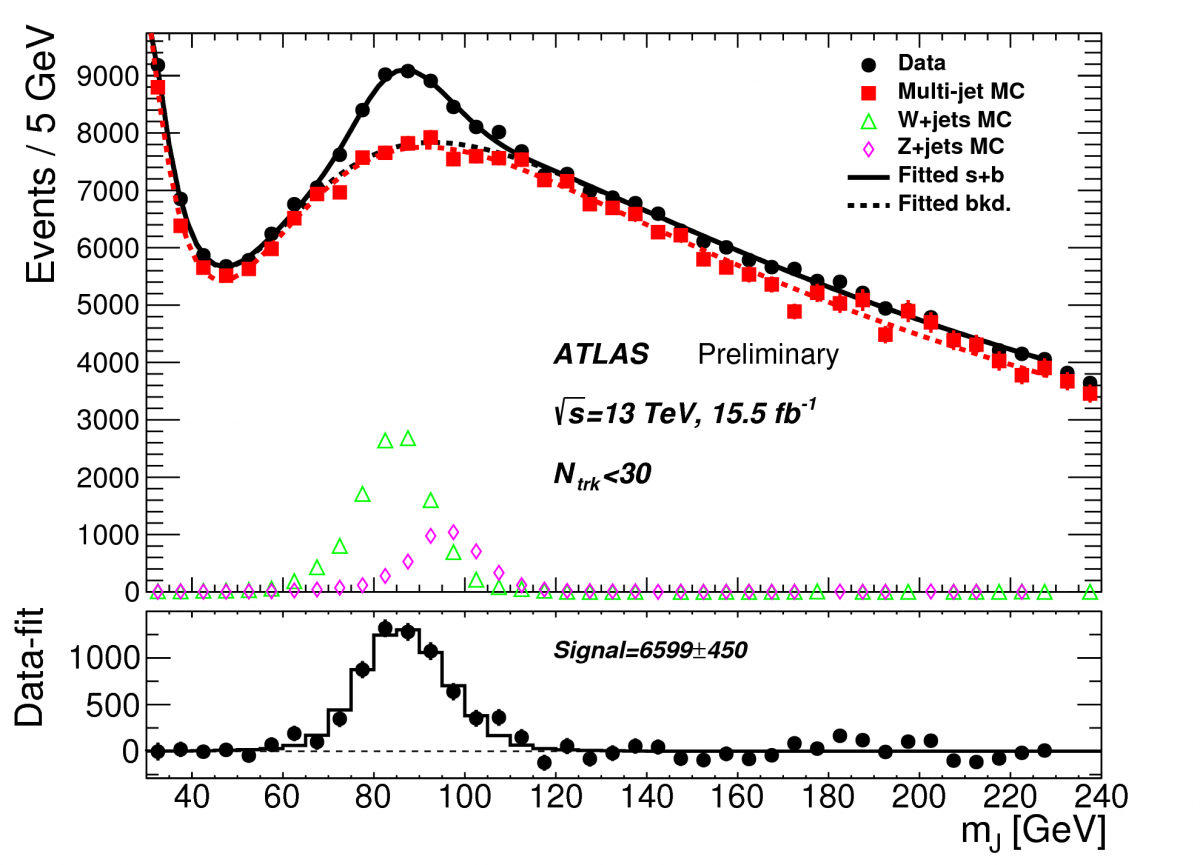
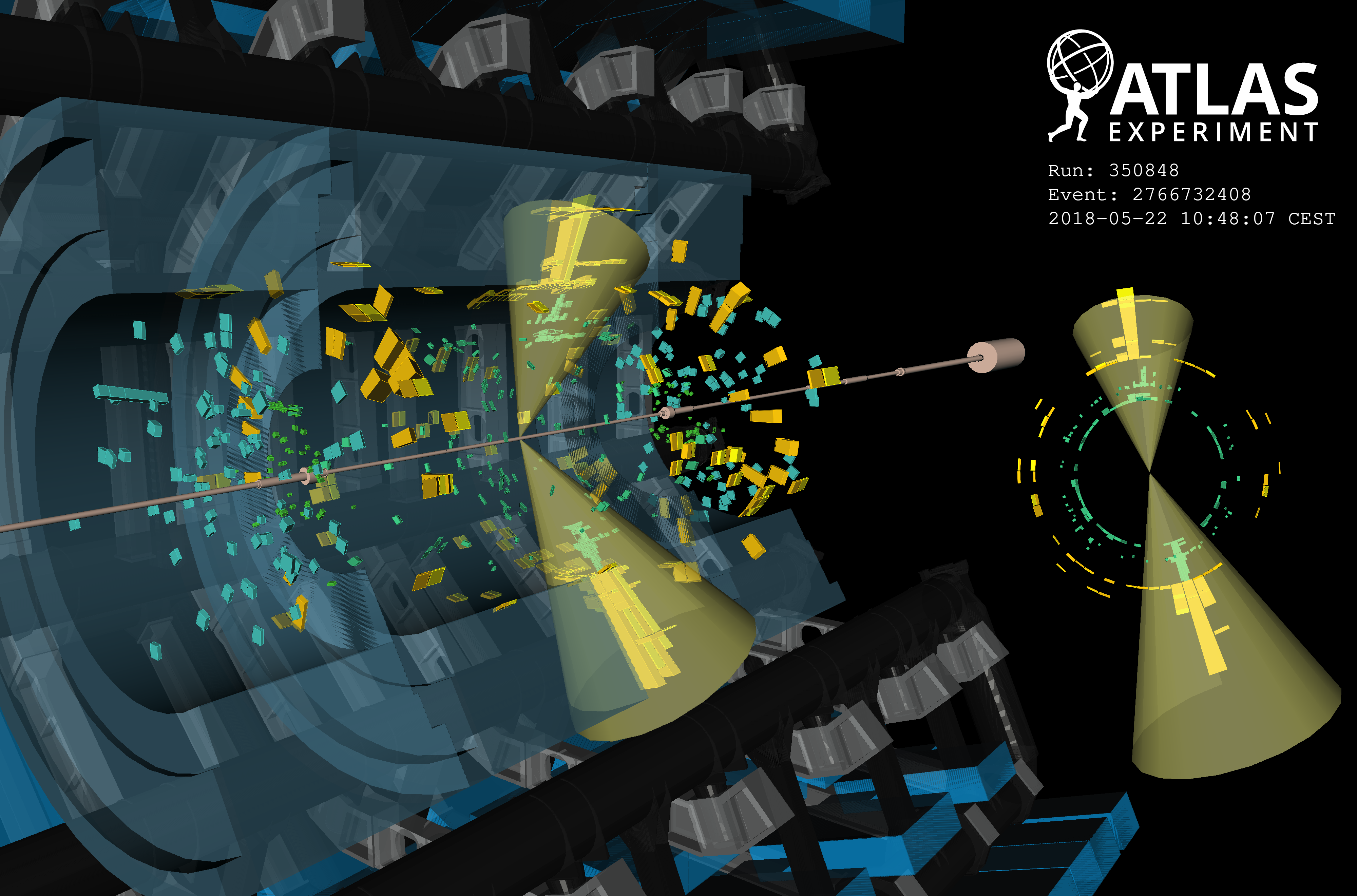
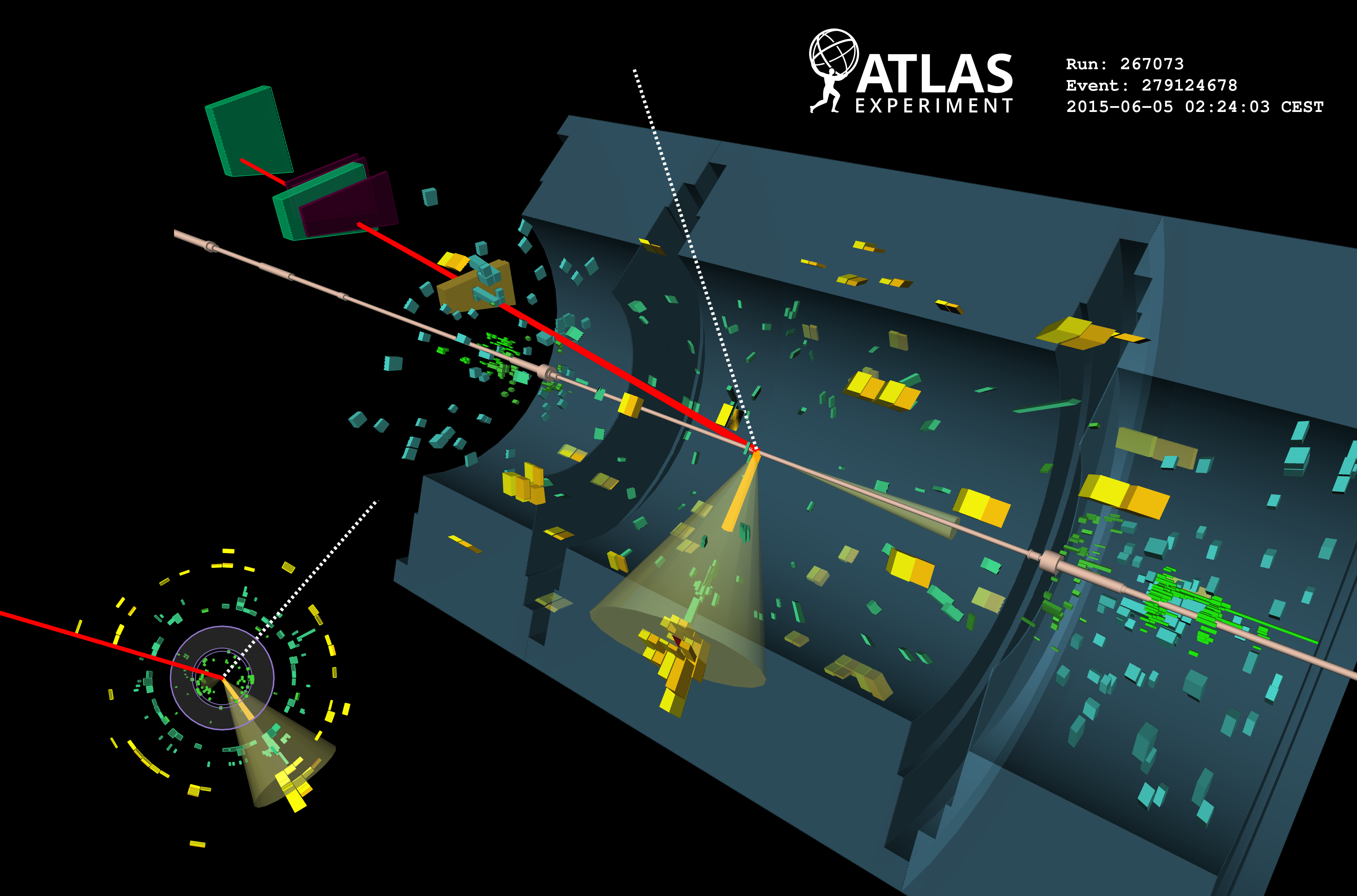
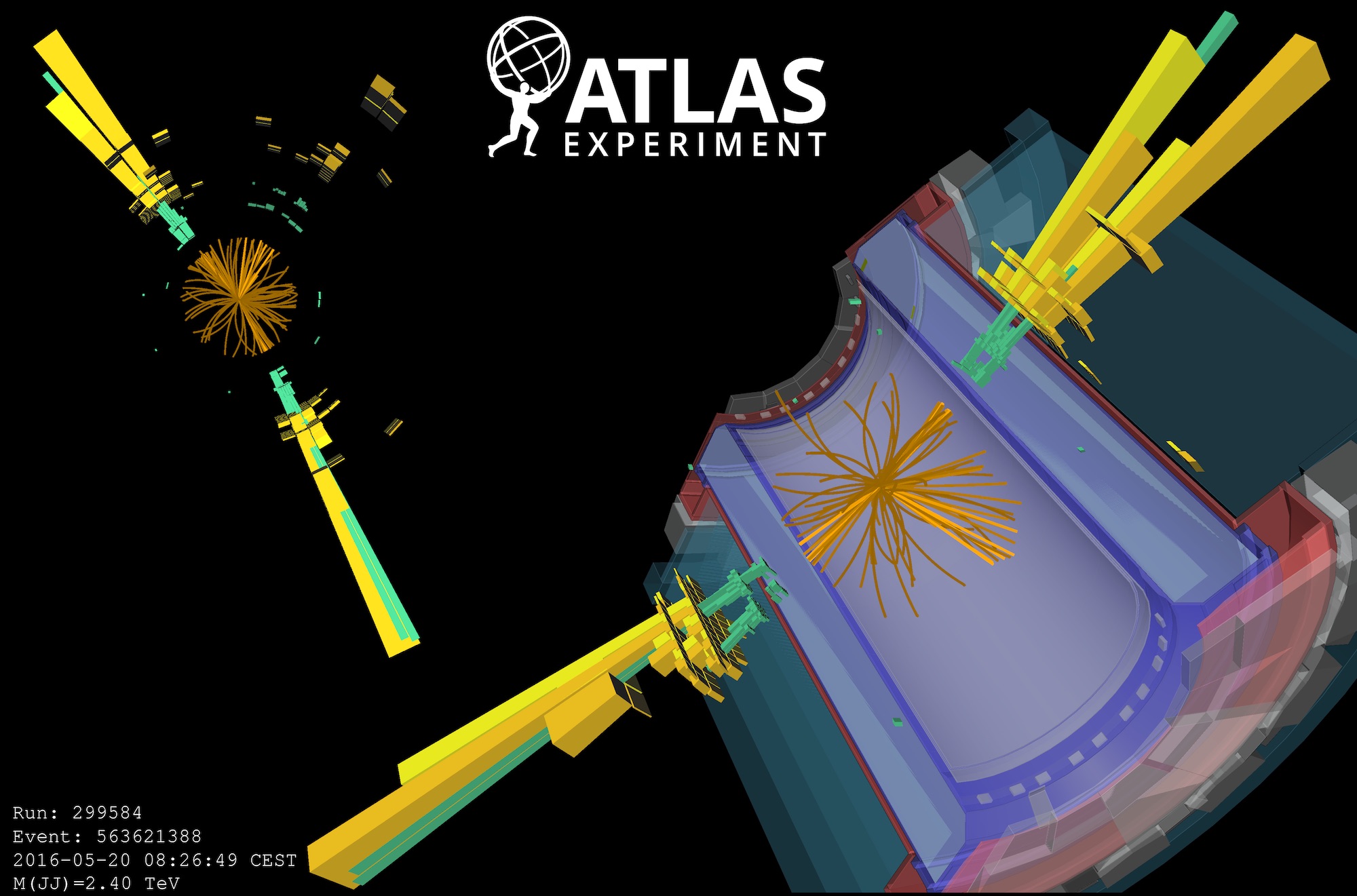
Figure 2: Distribution of the mass of the large jets in fully hadronic W/Z+jets events. The W/Z contribution (green) is extracted from the large multijet background (shown in red) after performing a fit to the data (shown in black). (Image: ATLAS Experiment/CERN)

One of the most direct ways to search for the unexpected is to look for new particles, often with multi-TeV mass. These heavy particles are featured in beyond the Standard Model theories and could be created at the Large Hadron Collider. Many of these new heavy particles may decay to pairs of bosons, such as W and Z bosons – discovered at CERN in 1983 – and the Higgs boson – discovered in 2012. Using relatively new techniques exploiting the internal structure of the jet (Figure 1), we are now able to reconstruct bosons decaying to jets with high precision (Figure 2), and can test a host of theories.

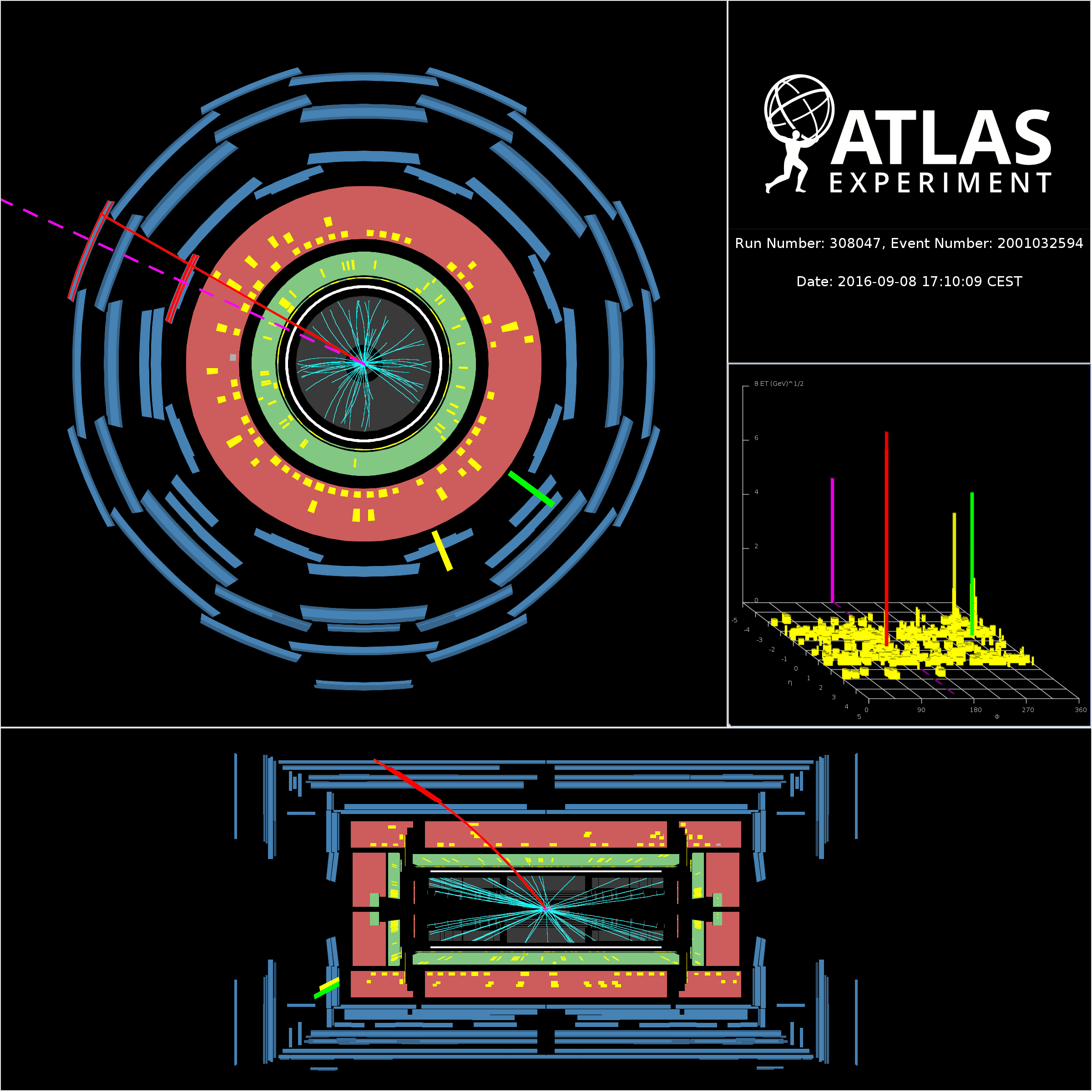
Using the available portion of the growing Run 2 dataset, the ATLAS experiment has analysed most of the decay modes of the W, Z gauge bosons and the Higgs boson: from fully hadronic modes, where both gauge bosons or Higgs decay to jets; to semi-leptonic modes, where one gauge boson decays to charged leptons; to missing energy modes, where one Z decays to neutrinos that then escape detection. All these searches look in a very general way for a peak over the smoothly falling Standard Model background (Figure 3). Sleepless nights are spent waiting for the data to go bump!

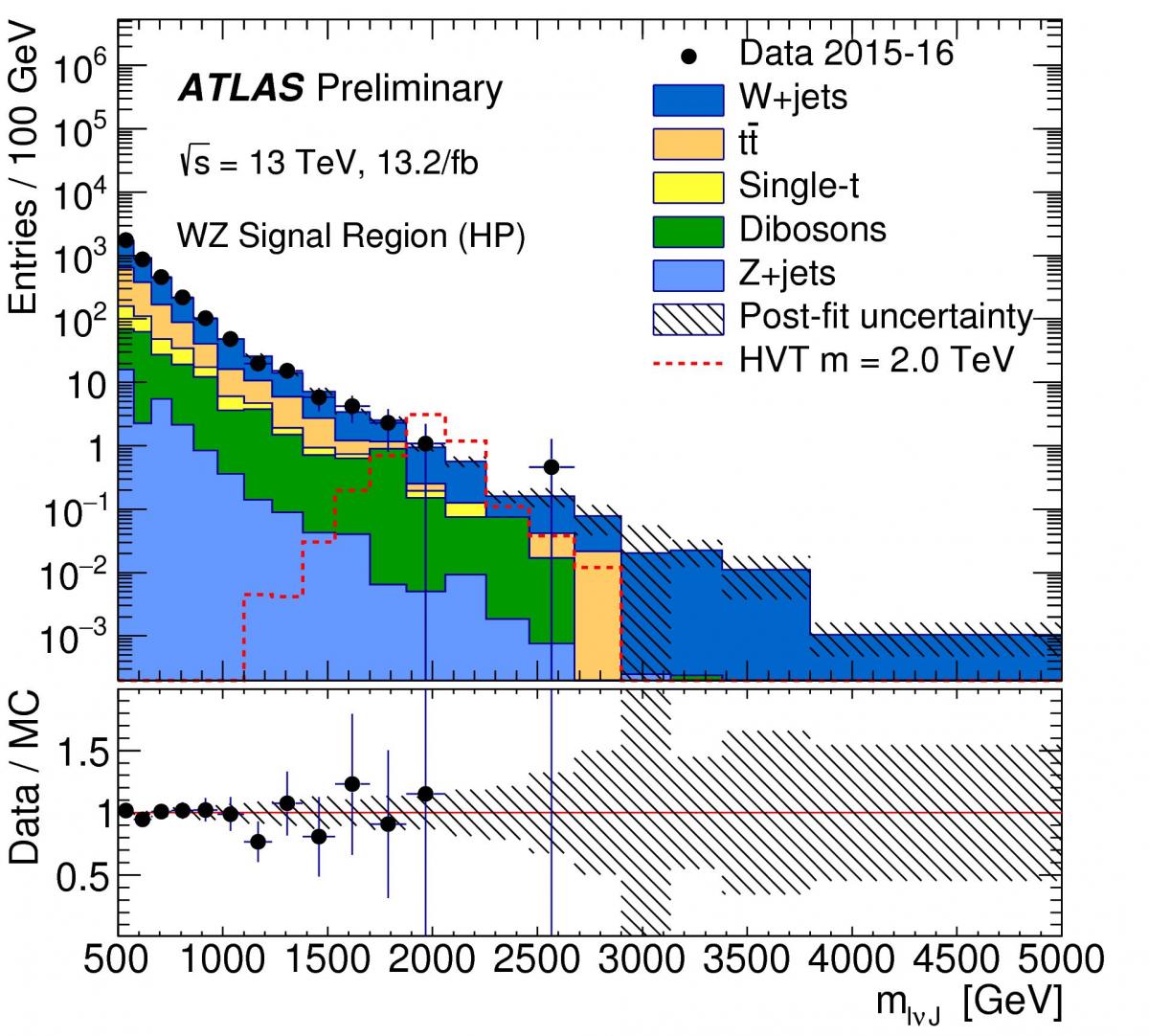
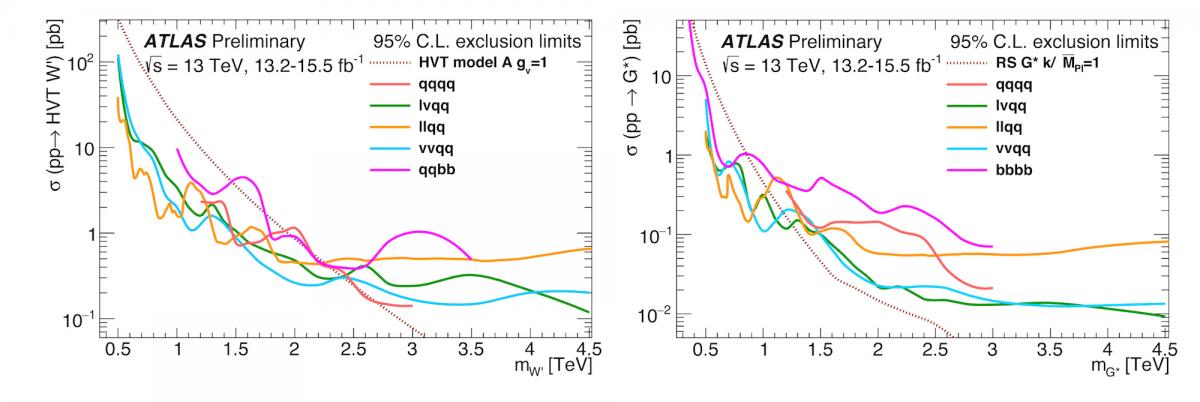
Figure 3: The final distributions for signal region focused on WZ decays where the W decays to a lepton and a neutrino and the Z decays to jets. The band shows the total statistical and systematic uncertainty on the background after the fitting to the data. The lower panels show the ratio of the observed data to the SM background estimation. No significant differences pointing to new physics are seen. (Image: ATLAS Experiment/CERN)

Unfortunately, no significant excess was found. Further constraints have been put on several theoretical models that motivate these searches, bounding the mass and cross section of new particles (Figure 4).

With the LHC running so well, we have already analysed nearly four times the 2015 data. By the end of this year, we expect to triple the amount analysed. This will further our search for heavier and more elusive particles. The unknown is waiting for us and the hunt for new physics is in full swing!