The first physics results from the ATLAS Experiment with proton-proton collisions at an energy of 0.9 TeV in late 2009 have now been accepted for publication in the journal Physics Letters B.

Almost 20 years since the inception of the ATLAS detector, the labors of 3000 scientists along with large numbers of engineers and other support staff have found fruition in the earliest results. These results demonstrate that this mammoth detector (seven stories tall and twice as long) works almost flawlessly. It is a great achievement that a 7000 tonne detector – with 3000 km of cables and close to 100 million channels to be read out – has successfully measured particle tracks with a precision of 0.001 centimeters so quickly.

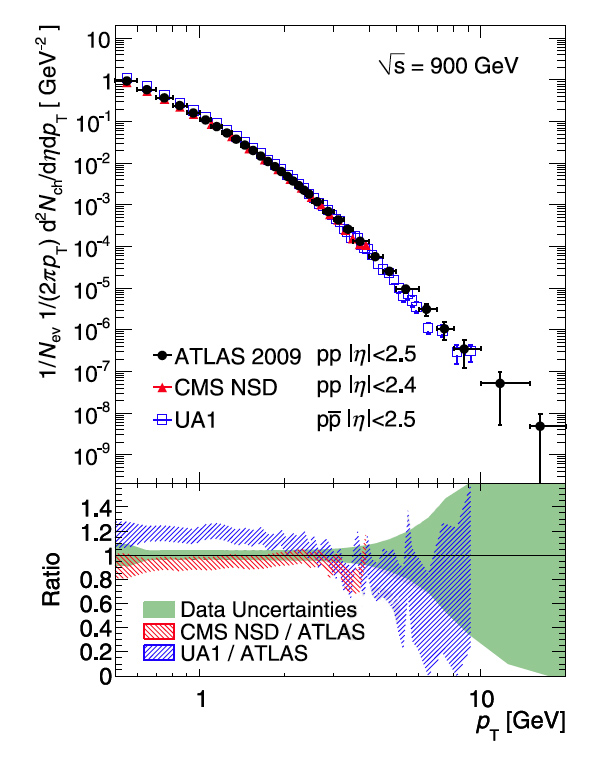
In later stages, ATLAS will focus on rare events and filter out less interesting events. This first paper reports on results with the “trigger” set to accept almost all events (this setting is called “minimum bias”). The paper reports results for the number of charged particles per collision and its dependence on several variables such as the particles’ momentum perpendicular to the beam.

The results from over 300,000 proton-proton collisions were compared with sophisticated computer simulations and with results from other experiments at the same collision energy. These comparisons demonstrate that the ATLAS detector performs remarkably well even at these early stages of the research. The inner detector of ATLAS (which follows the tracks of the charged particles emerging from the collisions) was key to the measurements. Data from the inner detector matched the simulations excellently.

Tom LeCompte, the Physics Coordinator for ATLAS, commented that: “It's particularly gratifying that our result be published now, on the eve of the LHC beginning its multi-year program of the highest energy collisions in the world. Teamwork was essential in being able to produce a physics result this quickly, especially with a brand new detector as complex as ATLAS.”

This first ATLAS paper with physics results represents a major milestone for the experiment at the Large Hadron Collider. It demonstrates the enormous potential for making major discoveries in the years ahead.

ATLAS spokesperson, Fabiola Gianotti, noted that "This first paper is very special for all of us, as it marks the beginning of a very exciting era of physics results and hopefully great discoveries. I am particularly delighted by the fact that the analysis described in this paper was mainly done by students and young post-docs. We are all very proud of these achievements."

Links

• Added 26 Apr 2010: Charged-particle multiplicities in 900 GeV pp interactions at measured with the ATLAS detector at the LHC (Physics Letters B 688 (2010) 21–42)