Probing Higgs boson production properties
17 July 2014 | By
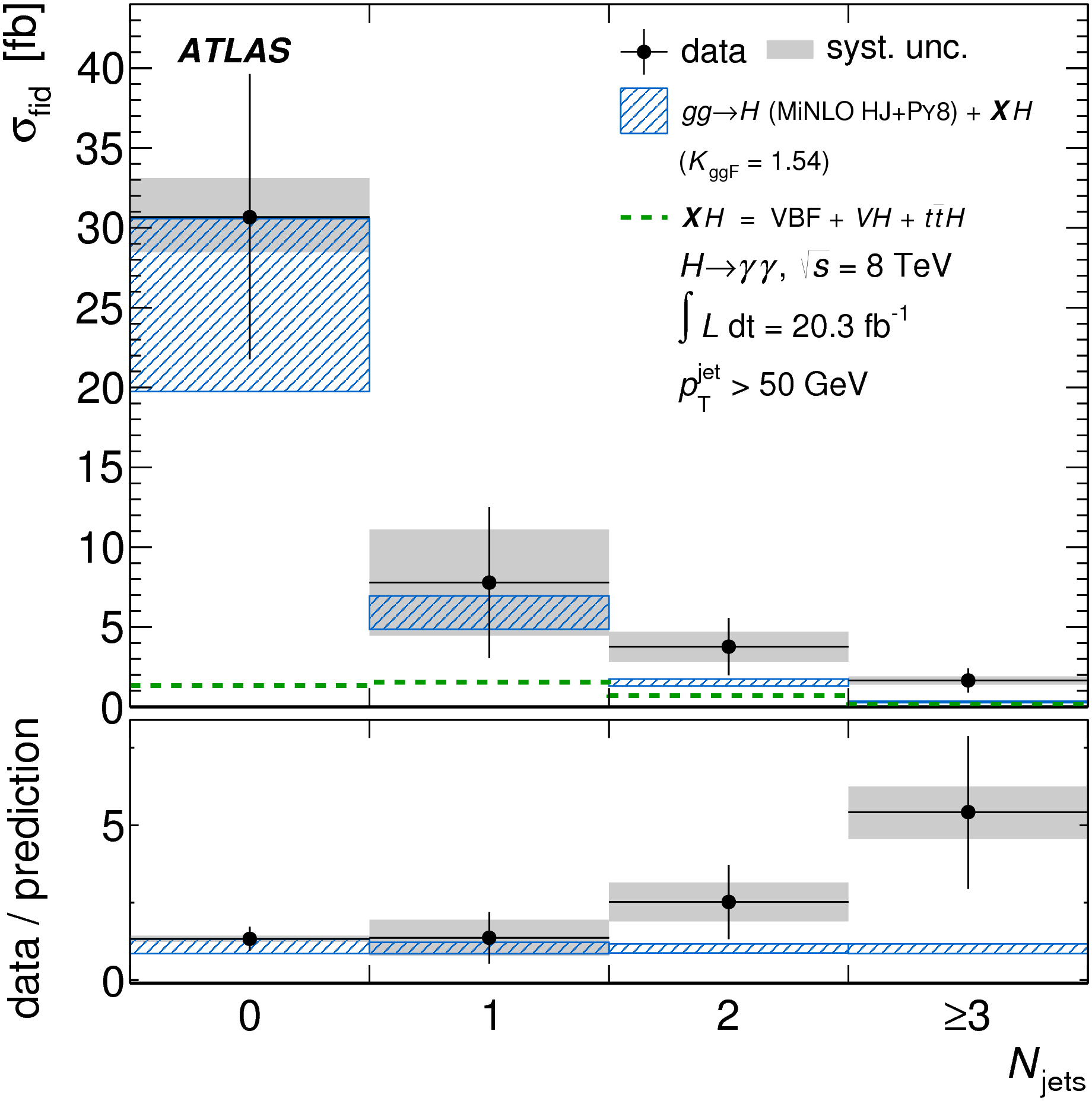
ATLAS has measured properties of events likely to contain a Higgs boson, in order to get a better understanding of the frequency and manner in which they are produced. The study specifically examines the fiducial and differential cross sections for Higgs bosons that decay into two photons or into two Z bosons, using proton-proton collisions recorded by ATLAS in 2012.
The cross section is a measure of the likelihood for Higgs boson production and its subsequent decay. Collisions that may contain a Higgs boson are identified in a narrow mass peak, constructed from the energy of two photons or the four leptons originating from the decay of the two Z bosons. The cross section is then determined from the observed signal yield after correcting the effects of detector inefficiency and resolution.
The cross section measurements in this study are designed to be as model independent as possible, to allow comparison to the best currently available theoretical predictions and improved theoretical predictions in the future.
Links:
- ATLAS conference note: Higgs to ZZ
- arXiv paper: Measurements of fiducial and differential cross sections for Higgs boson production in the diphoton decay channel at s√=8 TeV with ATLAS